题目内容
己知命题p:方程
+
=1表示焦点在y轴上的椭圆,命题q:方程
+
=1表示双曲线.如果p∨q为真,p∧q为假,求实数k的取值范围.
| x2 |
| 5-k |
| y2 |
| k+1 |
| x2 |
| 5-k |
| y2 |
| k+1 |
考点:双曲线的标准方程,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由p∨q为真,p∧q为假,知p,q为一真一假.由此能求出k的范围.
解答:
解:p:由k+1>5-k>0,得2<k<5,
q:由(5-k)(k+1)<0,得k<-1或k>5.(4分)
由p∨q为真,p∧q为假,知p,q为一真一假.
若p真q假,则
即2<k<5.
若p假q真,则
即k<-1或k>5.
综上,所求k的范围是:(-∞,-1)∪(2,5)∪(5,+∞).(8分)
q:由(5-k)(k+1)<0,得k<-1或k>5.(4分)
由p∨q为真,p∧q为假,知p,q为一真一假.
若p真q假,则
|
若p假q真,则
|
综上,所求k的范围是:(-∞,-1)∪(2,5)∪(5,+∞).(8分)
点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意椭圆和双曲线性质的合理运用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
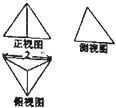
如图是各条棱长均为2的正四面体的三视图,则正视图三角形的面积为( )

A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
若某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )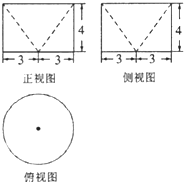

| A、33πcm2 |
| B、42πcm2 |
| C、48πcm2 |
| D、52πcm2 |
过椭圆
+
=1(a>b>0)的两个焦点作垂直x轴的直线与椭圆有四个交点,这四个交点恰好为正方形的四个顶点,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将7个红球,6个白球(小球只有颜色的区别)放入5个不同盒子,要求每个盒子中至少红球、白球各一个,则不同的放法共有( )
| A、20种 | B、25种 |
| C、45种 | D、75种 |