题目内容
在?ABCD中,O是对角线AC与BD的交点,E是BC边的中点,连接DE交AC于点F.已知
=
,
=
,则
= (用
和
表示)
| AB |
| a |
| AD |
| b |
| OF |
| a |
| b |
考点:向量的加法及其几何意义,向量的减法及其几何意义
专题:平面向量及应用
分析:首先,设
=λ
,
=μ
,(λ,μ为常数),然后,利用所给
=
,
=
,表示已知的向量,然后,结合向量的加法和减法运算表示即可.
| AF |
| AC |
| DF |
| DE |
| AB |
| a |
| AD |
| b |
解答:
解: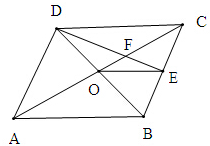
如图示,设
=λ
,
=μ
,(λ,μ为常数),
∴
-
=μ(
+
+
),
即λ
-
=μ(-
+
+
),
∴λ(
+
)-
=μ(
-
),
∴(λ-μ)
+(λ+
-1)
=
,
∵
,
不共线,
∴
,
∴λ=μ=
,
∵
=
-
=
-
=
=
(
+
)=
+
,
故答案为:
+
.

如图示,设
| AF |
| AC |
| DF |
| DE |
∴
| AF |
| AD |
| DA |
| AB |
| BE |
即λ
| AC |
| AD |
| b |
| a |
| 1 |
| 2 |
| b |
∴λ(
| a |
| b |
| b |
| a |
| 1 |
| 2 |
| b |
∴(λ-μ)
| a |
| μ |
| 2 |
| b |
| 0 |
∵
| a |
| b |
∴
|
∴λ=μ=
| 2 |
| 3 |
∵
| OF |
| AF |
| AO |
| 2 |
| 3 |
| AC |
| 1 |
| 2 |
| AC |
=
| 1 |
| 6 |
| AC |
| 1 |
| 6 |
| a |
| b |
| 1 |
| 6 |
| a |
| 1 |
| 6 |
| b |
故答案为:
| 1 |
| 6 |
| a |
| 1 |
| 6 |
| b |
点评:本题重点考查了平面向量基本定理和向量的加法和减法运算及其运算律等知识,属于中档题.巧妙利用共线条件是解题关键.

练习册系列答案
相关题目
下列四个关系式中,正确的是( )
| A、1∈{1,2} |
| B、1⊆{1,2} |
| C、{1}∈{1,2} |
| D、{1}={1,2} |
如图是各条棱长均为2的正四面体的三视图,则正视图三角形的面积为( )
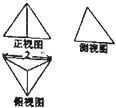

A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
已知实数a,b满足1003a+1004b=2006b,997a+1009b=2007a,则a与b的大小关系为( )
| A、a<b | B、a>b |
| C、a≤b | D、a≥b |
已知函数f(x)=sin(x+ϕ)+cos(x+ϕ)为偶函数,则ϕ的一个取值为( )
| A、0 | ||
B、
| ||
C、
| ||
| D、π |
若某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )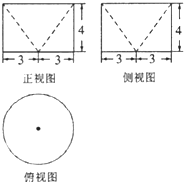

| A、33πcm2 |
| B、42πcm2 |
| C、48πcm2 |
| D、52πcm2 |