题目内容
已知函数f(x)=lnx,g(x)=ex
(1)若函数φ(x)=-x+f(-x),当x∈[-e,0)时,求φ(x)的值域.
(2)设直线l为函数f(x)的图象上一点A(x0,f(x0))处切线.证明:在区间(1,+∞)上存在唯一的x0使得直线l与曲线y=g(x)相切.
(1)若函数φ(x)=-x+f(-x),当x∈[-e,0)时,求φ(x)的值域.
(2)设直线l为函数f(x)的图象上一点A(x0,f(x0))处切线.证明:在区间(1,+∞)上存在唯一的x0使得直线l与曲线y=g(x)相切.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)求出原函数的导函数,由x的范围得到导函数的符号,进一步得到原函数的单调性,从而求得函数的值域;
(2):由f′(x)=
,求得切线l的方程y=
x+lnx0-1,设直线l与曲线y=g(x)相切于点(x1,ex1),由ex1=
说明l也为函数y=g(x)的切线,然后证明在区间(1,+∞)上x0存在且唯一即可.
(2):由f′(x)=
| 1 |
| x |
| 1 |
| x0 |
| 1 |
| x0 |
解答:
(1)解:当x∈[-e,0)时,φ(x)=-x+f(-x),
φ′(x)=-1+
=
,
∵x∈[-e,0),φ′(x)=-1+
=
<0,
∴φ(x)在[-e,0)上单调递减,
∴φ(x)∈(-∞,e+1];
(2)证明:∵f′(x)=
,
∴f′(x0)=
,
∴切线l的方程y-lnx0=
(x-x0),
即y=
x+lnx0-1 ①,
设直线l与曲线y=g(x)相切于点(x1,ex1),
∵g′(x)=ex,
∴ex1=
,则x1=-lnx0,
∴直线l也为y-
=
(x+lnx0),
即y=
x+
+
②,
由①②得,lnx0-1=
+
,
∴lnx0=
.
下面证明在区间(1,+∞)上x0存在且唯一.
φ′(x)=
+
=
.
∵x>0且x≠1,
∴φ′(x)>0.
∴函数φ(x)的单调递增区间为(0,1),(1,+∞),
可知,φ(x)=lnx-
在区间(1,+∞)上递增.
又φ(e)=lne-
=
<0,φ(e2)=lne2-
=
>0.
结合零点存在性定理,说明方程φ(x)=0必在区间(e,e2)上有唯一的根,这个根就是所求的唯一x0.
故结论成立.
φ′(x)=-1+
| 1 |
| x |
| 1-x |
| x |
∵x∈[-e,0),φ′(x)=-1+
| 1 |
| x |
| 1-x |
| x |
∴φ(x)在[-e,0)上单调递减,
∴φ(x)∈(-∞,e+1];
(2)证明:∵f′(x)=
| 1 |
| x |
∴f′(x0)=
| 1 |
| x0 |
∴切线l的方程y-lnx0=
| 1 |
| x0 |
即y=
| 1 |
| x0 |
设直线l与曲线y=g(x)相切于点(x1,ex1),
∵g′(x)=ex,
∴ex1=
| 1 |
| x0 |
∴直线l也为y-
| 1 |
| x0 |
| 1 |
| x0 |
即y=
| 1 |
| x0 |
| lnx0 |
| x0 |
| 1 |
| x0 |
由①②得,lnx0-1=
| lnx0 |
| x0 |
| 1 |
| x0 |
∴lnx0=
| x0+1 |
| x0-1 |
下面证明在区间(1,+∞)上x0存在且唯一.
φ′(x)=
| 1 |
| x |
| 2 |
| (x-1)2 |
| x2+1 |
| x(x-1)2 |
∵x>0且x≠1,
∴φ′(x)>0.
∴函数φ(x)的单调递增区间为(0,1),(1,+∞),
可知,φ(x)=lnx-
| x+1 |
| x-1 |
又φ(e)=lne-
| e+1 |
| e-1 |
| -2 |
| e-1 |
| e2+1 |
| e2-1 |
| e2-3 |
| e2-1 |
结合零点存在性定理,说明方程φ(x)=0必在区间(e,e2)上有唯一的根,这个根就是所求的唯一x0.
故结论成立.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,考查了存在性和唯一性的证明问题,是压轴题.

练习册系列答案
相关题目
如图是各条棱长均为2的正四面体的三视图,则正视图三角形的面积为( )

A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
过椭圆
+
=1(a>b>0)的两个焦点作垂直x轴的直线与椭圆有四个交点,这四个交点恰好为正方形的四个顶点,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
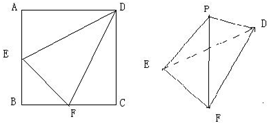 边长为2的正方形ABCD中,E∈AB,F∈BC
边长为2的正方形ABCD中,E∈AB,F∈BC 已知A,B是椭圆C:
已知A,B是椭圆C: