题目内容
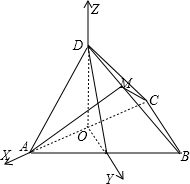
如图,在直角梯形ABCD中,AB=2CD=2AD,AD⊥AB,将△ADC沿AC这起,使平面ADC⊥平面ABC,得到几何体D-ABC.

(Ⅰ)求证:BC⊥AD;
(Ⅱ)点M是线段DB上的一点,当二面角M-AC-D的大小为时
时,求
的值.

(Ⅰ)求证:BC⊥AD;
(Ⅱ)点M是线段DB上的一点,当二面角M-AC-D的大小为时
| π |
| 3 |
| DM |
| NB |
考点:二面角的平面角及求法,平面与平面垂直的性质
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(Ⅰ)首先根据折叠问题,通过面面的垂直关系转化为线面垂直,通过相关的运算,进一步转化出线线垂直.
(Ⅱ)首先建立空间直角坐标系,进一步求出点的坐标,然后分别求出平面的法向量,设
=λ
,进一步根据二面角cos
=
=
,求得λ的值.
(Ⅱ)首先建立空间直角坐标系,进一步求出点的坐标,然后分别求出平面的法向量,设
| DM |
| DB |
| π |
| 3 |
| ||||
|
|
| 1 |
| 2 |
解答:
(Ⅰ)证明:∵平面ACD⊥平面ABC=AC
∴在直角梯形ABCD中,AB=2CD=2AD,AD⊥AB
求得:BC⊥AC
∴BC⊥平面ACD
AD?平面ACD
∴BC⊥AD
(Ⅱ)分别取AC、AB的中点O、E,分别以OA、OE、OD为x轴,y轴,z轴建立空间直角坐标系,设AD=
则:A(1,0,0),C(-1,0,0),D(0,O,1),B(-1,2,0)
设
=λ
,M(x,y,z)则:x=-λ,y=2λ,z=1-λ
所以:
=(-2,0,0),
=(-λ-1,2λ,1-λ)
设平面AMC的法向量
=(x,y,z)
则有:
得到:
令z=2λ
则:x=0,y=λ-1
又平面ADC的法向量
=(0,1,0)
由题意可知:当二面角M-AC-D的大小为
时,
cos
=
=
解得:
=
λ=2
-3
即
=(2
-3)
所以:
=
∴在直角梯形ABCD中,AB=2CD=2AD,AD⊥AB
求得:BC⊥AC
∴BC⊥平面ACD
AD?平面ACD
∴BC⊥AD
(Ⅱ)分别取AC、AB的中点O、E,分别以OA、OE、OD为x轴,y轴,z轴建立空间直角坐标系,设AD=
| 2 |
则:A(1,0,0),C(-1,0,0),D(0,O,1),B(-1,2,0)
设
| DM |
| DB |
所以:
| AC |
| AM |
设平面AMC的法向量
| n1 |
则有:
|
得到:
|

令z=2λ
则:x=0,y=λ-1
又平面ADC的法向量
| n2 |
由题意可知:当二面角M-AC-D的大小为
| π |
| 3 |
cos
| π |
| 3 |
| ||||
|
|
| 1 |
| 2 |
解得:
| λ-1 | ||
|
| 1 |
| 2 |
λ=2
| 3 |
即
| DM |
| 3 |
| DB |
所以:
| DM |
| MB |
| ||
| 2 |
点评:本题考查的知识要点:面面垂直与线面垂直和线线垂直之间的转化及相关运算,法向量的应用,空间直角坐标系的建立技巧,向量共线的应用,二面角的应用.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
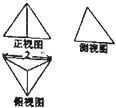
如图是各条棱长均为2的正四面体的三视图,则正视图三角形的面积为( )

A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
已知函数f(x)=sin(x+ϕ)+cos(x+ϕ)为偶函数,则ϕ的一个取值为( )
| A、0 | ||
B、
| ||
C、
| ||
| D、π |
