题目内容
设a0+
a1+
a2+…+
an=0,其中ai(i=0,1,…n)是不全为零的常数,试证明:多项式f(x)=a0+a1x+…+anxn在(0,1)内至少有一个零点.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:令g(x)=∫f(x)dx=∫(a0+a1x+…+anxn)dx=a0x+
x2+
x3+…+
xn+1,显然g(0)=0,g(1)=a0+
a1+
a2+…+
an=0,从而解决问题.
| a1 |
| 2 |
| a2 |
| 3 |
| an |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
解答:
证明:已知a0+
a1+
a2+…+
an=0,f(x)=a0+a1x+…+anxn,
令g(x)=∫f(x)dx=∫(a0+a1x+…+anxn)dx=a0x+
x2+
x3+…+
xn+1,
显然g(0)=0,g(1)=a0+
a1+
a2+…+
an=0,
而g(x)在(0,1)内连续,且不恒等于0,∴g(x)在(0,1)至少存在一个极值,
故g′(x)=f(x)=a0+a1x+…+anxn=0在(0,1)内至少有1个实数根,
∴f(x)=a0+a1x+…+anxn在(0,1)内至少有一个零点.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
令g(x)=∫f(x)dx=∫(a0+a1x+…+anxn)dx=a0x+
| a1 |
| 2 |
| a2 |
| 3 |
| an |
| n+1 |
显然g(0)=0,g(1)=a0+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
而g(x)在(0,1)内连续,且不恒等于0,∴g(x)在(0,1)至少存在一个极值,
故g′(x)=f(x)=a0+a1x+…+anxn=0在(0,1)内至少有1个实数根,
∴f(x)=a0+a1x+…+anxn在(0,1)内至少有一个零点.
点评:本题考查了函数的零点的判定定理,考查了不定积分的应用,是一道中档题.

练习册系列答案
相关题目
下列各命题正确的是( )
| A、终边相同的角一定相等 | ||||||||
| B、若α是第四象限的角,则π-α在第三象限 | ||||||||
C、若|
| ||||||||
| D、若α∈(0,π),则sinα>cosα |
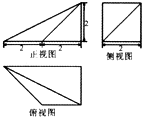
某几何体的三视图如图所示,则这个几何体的体积为( )

A、
| ||
B、
| ||
| C、8 | ||
| D、4 |