题目内容
函数y=3-sinx-2cos2x的值域为 .
考点:复合三角函数的单调性
专题:三角函数的求值
分析:由三角函数知识化简可得y=2(sinx-
)2+
,令sinx=t,则t∈[-1,1],研究二次函数y=2(t-
)2+
的单调性和值域即可.
| 1 |
| 4 |
| 7 |
| 8 |
| 1 |
| 4 |
| 7 |
| 8 |
解答:
解:化简可得y=3-sinx-2cos2x
=3-sinx-2(1-sin2x)
=2sin2x-sinx+1
=2(sinx-
)2+
,
令sinx=t,则t∈[-1,1],
由二次函数可知y=2(t-
)2+
在t∈[-1,
]单调递减,在t∈[
,1]单调递增,
∴当t=
时,上取到最小值
,
当t=-1时,上取到最大值4
故答案为:[
,4]
=3-sinx-2(1-sin2x)
=2sin2x-sinx+1
=2(sinx-
| 1 |
| 4 |
| 7 |
| 8 |
令sinx=t,则t∈[-1,1],
由二次函数可知y=2(t-
| 1 |
| 4 |
| 7 |
| 8 |
在t∈[-1,
| 1 |
| 4 |
| 1 |
| 4 |
∴当t=
| 1 |
| 4 |
| 7 |
| 8 |
当t=-1时,上取到最大值4
故答案为:[
| 7 |
| 8 |
点评:本题考查复合三角函数的单调性和最值,换元是解决问题的关键,属基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
x2-x-6<0的解集是( )
| A、(-∞,-2)∪(3,+∞) |
| B、(-2,3) |
| C、(2,3) |
| D、(-3,2) |
要得到函数y=sin(2x+
)的图象,只需将函数y=sin2x的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
已知A={x|x2-3x-10≤0},B={x|x>3},则A∩B=( )
| A、{x|3<x≤5} |
| B、{x|3≤x≤5} |
| C、{x|-2≤x≤3} |
| D、{x|x>3} |
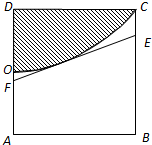 如图,有一边长为2米的正方形钢板ABCD缺损一角(图中的阴影部分),边缘线OC是以直线AD为对称轴,以线段AD的中点O为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
如图,有一边长为2米的正方形钢板ABCD缺损一角(图中的阴影部分),边缘线OC是以直线AD为对称轴,以线段AD的中点O为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.