题目内容

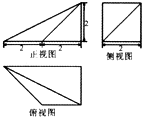
某几何体的三视图如图所示，则这个几何体的体积为（　　）
A、
20
3
B、
26
3
C、8
D、4
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得：该几何体是一个四棱锥和一个三棱锥组成的组合体，画出几何体的直观图，求出两个棱锥的体积，相加可得答案．
解答： 解：由已知中的三视图可得该几何体的直观图如下图所示：

该几何体是一个四棱锥A-CDEF和一个三棱锥组F-ABC成的组合体，
四棱锥A-CDEF的底面面积为4，高为4，故体积为：
16
3
，
三棱锥组F-ABC的底面面积为2，高为2，故体积为：
4
3
，
故这个几何体的体积V=
16
3
+
4
3
=
20
3
，
故选：A
点评：根据三视图判断空间几何体的形状，进而求几何的表（侧/底）面积或体积，是高考必考内容，处理的关键是准确判断空间几何体的形状，一般规律是这样的：如果三视图均为三角形，则该几何体必为三棱锥；如果三视图中有两个三角形和一个多边形，则该几何体为N棱锥（N值由另外一个视图的边数确定）；如果三视图中有两个为矩形和一个多边形，则该几何体为N棱柱（N值由另外一个视图的边数确定）；如果三视图中有两个为梯形和一个多边形，则该几何体为N棱柱（N值由另外一个视图的边数确定）；如果三视图中有两个三角形和一个圆，则几何体为圆锥．如果三视图中有两个矩形和一个圆，则几何体为圆柱．如果三视图中有两个梯形和一个圆，则几何体为圆台．
练习册系列答案
相关题目
设集合S={x||x|＜5}，T={x|x2+4x-21＜0}，则S∩T=（　　）
A、{x|-7＜x＜-5}
B、{x|3＜x＜5}
C、{x|-5＜x＜3}
D、{x|-7＜x＜5}
设函数f（x）=
x2+1
-ax，（a＞0），试确定：当a取什么值时，函数f（x）在[0，+∞）上为单调函数．
已知曲线C：
x2
a
2
n
-y2=1（an＞0，n∈N*）的一个焦点为F（
n2+1
，0）．
（1）求an，
（2）令bn=
1
anan+1
，Tn=b1+b2+…+bn，求Tn．
设a0+
1
2
a1+
1
3
a2+…+
1
n+1
an=0，其中ai（i=0，1，…n）是不全为零的常数，试证明：多项式f（x）=a0+a1x+…+anxn在（0，1）内至少有一个零点．
已知定点A、B，且|AB|=2，动点P满足|PA|-|PB|=1，则点P的轨迹为（　　）
A、双曲线B、双曲线一支
C、两条射线D、一条射线
已知数列{an}，a1=1且an-1-an=an-1an（n≥2，n∈N*），则Tn=a1a2+a2a3+…+anan-1的值为
 
．
若函数f（x）=Asin（ωx+
π
2
）+b（A＞0，ω＞0）的最小正周期为
π
2
，在一个周期内最大值和最小值之和为2，且方程f（x）=A的三个最小的不同正根按照从小到大的顺序恰好构成等比数列．
（1）试求函数f（x）的解析式；
（2）将y=f（x）的图象向下平移一个单位，再向左平移
π
12
个单位，得到函数y=g（x），试在如图所给的直角坐标系中画出函数y=g（x）在一个周期内的图象．
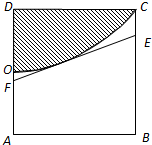如图，有一边长为2米的正方形钢板ABCD缺损一角（图中的阴影部分），边缘线OC是以直线AD为对称轴，以线段AD的中点O为顶点的抛物线的一部分．工人师傅要将缺损一角切割下来，使剩余的部分成为一个直角梯形．
（1）请建立适当的直角坐标系，求阴影部分的边缘线OC的方程；
（2）如何画出切割路径EF，使得剩余部分即直角梯形ABEF的面积最大？
并求其最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网