题目内容
已知O是△ABC内一点，若
+2
+3
=
，则△AOC与△ABC的面积的比值为（ ）
| OA |
| OB |
| OC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：由
+2
+3
=
变形为
+3
=-2
．以
、3
所在的线段OA、OE为邻边作平行四边形OAFE．
设对角线OF与AC交与点D．利用向量的平行四边形法则和平行四边形的性质可得
=
．进而得出．
| OA |
| OB |
| OC |
| 0 |
| OA |
| OC |
| OB |
| OA |
| OC |
设对角线OF与AC交与点D．利用向量的平行四边形法则和平行四边形的性质可得
| OD |
| BD |
| 1 |
| 3 |
解答：
解：如图所示，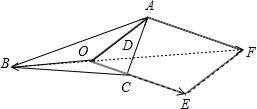
由
+2
+3
=
变形为
+3
=-2
．
以
、3
所在的线段OA、OE为邻边作平行四边形OAFE．
设对角线OF与AC交与点D．
则
=-2
．
∴
=
=
，
∴
=
，化为
=
，即
=
．
∴△AOC与△ABC的面积的比值=
．
故选：C．
由
| OA |
| OB |
| OC |
| 0 |
| OA |
| OC |
| OB |
以
| OA |
| OC |
设对角线OF与AC交与点D．
则
| OF |
| OB |
∴
| OD |
| DF |
| OC |
| AF |
| 1 |
| 3 |
∴
| OD |
| 2OB-OD |
| 1 |
| 3 |
| OD |
| OB |
| 1 |
| 2 |
| OD |
| BD |
| 1 |
| 3 |
∴△AOC与△ABC的面积的比值=
| 1 |
| 3 |
故选：C．
点评：本题考查了向量的平行四边形法则和平行四边形的性质，考查了作辅助线的重要性和技巧，属于难题．
练习册系列答案
口算题天天练系列答案
相关题目
若复数z满足（1+i）z=1+2i（其中i是虚数单位），则复数z对应的点位于复平面的（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列函数是奇函数的是（ ）
| A、f（x）=-|x| |
| B、f（x）=lg（1+x）-lg（1-x） |
| C、f（x）=2x+2-x |
| D、f（x）=x3-1 |
如图，正方体的棱长为1，线段B′D′上有两个动点E，F，EF=| 1 |
| 2 |
| A、AC⊥BE |
| B、EF∥平面ABCD |
| C、三棱锥A-BEF的体积为定值 |
| D、异面直线AE，BF所成角为定值 |
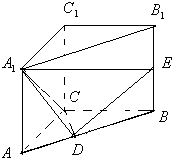已知直三棱柱ABC-A1B1C1中，∠ACB=