题目内容
若复数z满足（1+i）z=1+2i（其中i是虚数单位），则复数z对应的点位于复平面的（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：直接化简复数（1+i）z=1+2i为a+bi的形式，即可确定复数在复平面内对应的点所在象限．
解答：
解：∵（1+i）z=1+2iz
=
=
，复数z在复平面内对应的点为（
，
），
∴复数z在复平面内对应的点在第一象限．
故选：A．
| 1+2i |
| 1+i |
| (1+2i)(1-i) |
| (1+i)(1-i) |
| 3+I |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴复数z在复平面内对应的点在第一象限．
故选：A．
点评：本题考查复数的基本运算，复数的几何意义，考查计算能力．
练习册系列答案
相关题目
设全集U是实数集R，集合M={x|x2＞2x}，N={x|log2（x-1）≤0}，则（∁UM）∩N为（ ）
| A、{x|1＜x＜2} |
| B、{x|1≤x≤2} |
| C、{x|1＜x≤2} |
| D、{x|1≤x＜2} |
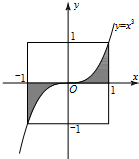如图，设D是图中边长为2的正方形区域，E是函数y=x3的图象与x轴及x=±1围成的阴影区域．向D中随机投一点，则该点落入E中的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知O是△ABC内一点，若
+2
+3
=
，则△AOC与△ABC的面积的比值为（ ）
| OA |
| OB |
| OC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图：已知直线与抛物线y2=2px（p＞0）交于A，B两点，且OA⊥OB，OD⊥AB交AB于点D，点D的坐标为（2，1）．