题目内容
下列函数是奇函数的是（ ）
| A、f（x）=-|x| |
| B、f（x）=lg（1+x）-lg（1-x） |
| C、f（x）=2x+2-x |
| D、f（x）=x3-1 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：先看定义域是否关于原点对称，再看f（-x）与f（x）的关系，从而根据奇函数、偶函数的定义作出判断．
解答：
解：对于函数f（x）=-|x|，由于f（-x）=-|-x|=-|x|=f（x），故函数f（x）为偶函数．
对于f（x）=lg（1+x）-lg（1-x），它的定义域为（-1，1），
且满足f（-x）=lg（1-x）-lg（1+x）=-f（x），故函数f（x）为奇函数．
对于函数f（x）=2x+2-x，由于f（-x）=2x+2-x=f（x），故函数f（x）为偶函数．
对于函数f（x）=x3-1，由于f（-x）=-x3-1≠-f（x），故不是奇函数，
故选：B．
对于f（x）=lg（1+x）-lg（1-x），它的定义域为（-1，1），
且满足f（-x）=lg（1-x）-lg（1+x）=-f（x），故函数f（x）为奇函数．
对于函数f（x）=2x+2-x，由于f（-x）=2x+2-x=f（x），故函数f（x）为偶函数．
对于函数f（x）=x3-1，由于f（-x）=-x3-1≠-f（x），故不是奇函数，
故选：B．
点评：本题主要考查函数的奇偶性的判断方法，先看定义域是否关于原点对称，再看f（-x）与f（x）的关系，属于中档题．
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，底面ABCD是矩形，已知AB=4，AD=2，PA=2，PD=2设全集U是实数集R，集合M={x|x2＞2x}，N={x|log2（x-1）≤0}，则（∁UM）∩N为（ ）
| A、{x|1＜x＜2} |
| B、{x|1≤x≤2} |
| C、{x|1＜x≤2} |
| D、{x|1≤x＜2} |
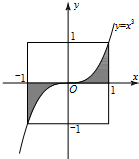如图，设D是图中边长为2的正方形区域，E是函数y=x3的图象与x轴及x=±1围成的阴影区域．向D中随机投一点，则该点落入E中的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x∈N|0＜x＜3}，B={x|2x-1＞1}，则A∩B=（ ）
| A、∅ | B、{1} |
| C、{2} | D、{1，2} |
已知O是△ABC内一点，若
+2
+3
=
，则△AOC与△ABC的面积的比值为（ ）
| OA |
| OB |
| OC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|