题目内容
已知椭圆M、抛物线N的焦点均在x轴上的,且M的中心和M的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:
(Ⅰ)求M,N的标准方程;
(Ⅱ)已知定点A(1,
),过原点O作直线l交椭圆M于B,C两点,求△ABC面积的最大值和此时直线l的方程.
| x | 3 | -2 | 4 |
| ||||||
| y | -2
|
0 | -4 |
|
(Ⅱ)已知定点A(1,
| 1 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设抛物线M:y2=2px(p≠0),则有
=2p(x≠0),据此验证4个点知(3,-2
),(4,-4)在抛物线上,可得N的标准方程,将另外两点代入椭圆方程,可求M的标准方程;
(Ⅱ)分类讨论,当直线BC不垂直于x轴时,设该直线方程为y=kx,代入椭圆方程,表示出面积,利用换元法,即可求得结论.
| y2 |
| x |
| 3 |
(Ⅱ)分类讨论,当直线BC不垂直于x轴时,设该直线方程为y=kx,代入椭圆方程,表示出面积,利用换元法,即可求得结论.
解答:
解:(Ⅰ)设抛物线M:y2=2px(p≠0),则有
=2p(x≠0)
据此验证4个点知(3,-2
),(4,-4)在抛物线上,
∴N的标准方程为y2=4x.…(2分)
设M:
+
=1(a>b>0),把点(-2,0),(
,
)
代入得:
,解得a2=4,b2=1
∴M的标准方程为
+y2=1; (6分)
(Ⅱ)当直线BC垂直于x轴时,BC=2,则S△ABC=1
当直线BC不垂直于x轴时,设该直线方程为y=kx,
代入椭圆方程,消y得x2=
不妨设B(
,
),C(-
,-
),
∴|BC|=
=
(9分)
∵点A到直线BC的距离d=
∴S△ABC=
|BC|×d=
=
=
,(12分)
令t=
,则4tk2-4k+t=0,
由△k=16-16t2≥0得-1≤t≤1
∴当
=-1时,面积取得最大值
,此时k=-
.
综上所述,当直线的方程为y=-
x时,△ABC的面积取得最大值
(14分)
| y2 |
| x |
据此验证4个点知(3,-2
| 3 |
∴N的标准方程为y2=4x.…(2分)
设M:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
代入得:
|
∴M的标准方程为
| x2 |
| 4 |
(Ⅱ)当直线BC垂直于x轴时,BC=2,则S△ABC=1
当直线BC不垂直于x轴时,设该直线方程为y=kx,
代入椭圆方程,消y得x2=
| 4 |
| 4k2+1 |
不妨设B(
| 2 | ||
|
| 2k | ||
|
| 2 | ||
|
| 2k | ||
|
∴|BC|=
| (xB-xA)2+(yB-yA)2 |
4
| ||
|
∵点A到直线BC的距离d=
|k-
| ||
|
∴S△ABC=
| 1 |
| 2 |
| |2k-1| | ||
|
| ||
|
1-
|
令t=
| 4k |
| 4k2+1 |
由△k=16-16t2≥0得-1≤t≤1
∴当
| 4k |
| 4k2+1 |
| 2 |
| 1 |
| 2 |
综上所述,当直线的方程为y=-
| 1 |
| 2 |
| 2 |
点评:本题考查抛物线、椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
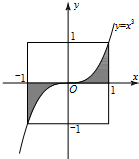 如图,设D是图中边长为2的正方形区域,E是函数y=x3的图象与x轴及x=±1围成的阴影区域.向D中随机投一点,则该点落入E中的概率为( )
如图,设D是图中边长为2的正方形区域,E是函数y=x3的图象与x轴及x=±1围成的阴影区域.向D中随机投一点,则该点落入E中的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知O是△ABC内一点,若
+2
+3
=
,则△AOC与△ABC的面积的比值为( )
| OA |
| OB |
| OC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 为监测幼儿身体发育状况,某幼儿园对“大班”的100名幼儿的体重做了测量,并根据所得数据画出了频率分布直方图,如图所示.则体重在[18,20](单位kg)的幼儿人数为( )
为监测幼儿身体发育状况,某幼儿园对“大班”的100名幼儿的体重做了测量,并根据所得数据画出了频率分布直方图,如图所示.则体重在[18,20](单位kg)的幼儿人数为( ) 如图:已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1).
如图:已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1).