题目内容
 如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF=
如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF=| 1 |
| 2 |
| A、AC⊥BE |
| B、EF∥平面ABCD |
| C、三棱锥A-BEF的体积为定值 |
| D、异面直线AE,BF所成角为定值 |
考点:命题的真假判断与应用,棱柱、棱锥、棱台的体积,异面直线及其所成的角,直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:由正方体的几何特征结合线面垂直的判定证得AC⊥面BB′D′D,从而得到AC⊥BE;
由线面平行的判定证明EF∥平面ABCD;
三棱锥A-BEF的底面三角形BEF的面积为定值,高AO为定值,从而得到三棱锥A-BEF的体积为定值.
排除前三项后可得答案为D.
由线面平行的判定证明EF∥平面ABCD;
三棱锥A-BEF的底面三角形BEF的面积为定值,高AO为定值,从而得到三棱锥A-BEF的体积为定值.
排除前三项后可得答案为D.
解答:
解:如图,
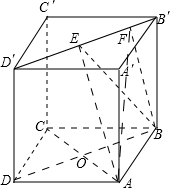
∵AC′是正方体,
∴底面ABCD为正方形,连结AC,则AC⊥BD,
又BB′⊥底面ABCD,
∴BB′⊥AC,
BB′∩BD=B,
∴AC⊥面BB′D′D,
∴AC⊥BE.选项A正确;
∵EF∥BD,BD?面ABCD,EF?面ABCD,
∴EF∥面ABCD.选项B正确;
∵△BEF的底EF=
,高为BB′=1,
∴S△BEF为定值.
又三棱锥A-BEF的高为AO为定值,
∴三棱锥A-BEF的体积为定值.选项C正确;
∴不正确的选项为D.
故选:D.

∵AC′是正方体,
∴底面ABCD为正方形,连结AC,则AC⊥BD,
又BB′⊥底面ABCD,
∴BB′⊥AC,
BB′∩BD=B,
∴AC⊥面BB′D′D,
∴AC⊥BE.选项A正确;
∵EF∥BD,BD?面ABCD,EF?面ABCD,
∴EF∥面ABCD.选项B正确;
∵△BEF的底EF=
| 1 |
| 2 |
∴S△BEF为定值.
又三棱锥A-BEF的高为AO为定值,
∴三棱锥A-BEF的体积为定值.选项C正确;
∴不正确的选项为D.
故选:D.
点评:本题考查命题的真假判断与应用,考查了空间点、线、面的位置关系,综合考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
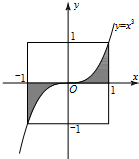 如图,设D是图中边长为2的正方形区域,E是函数y=x3的图象与x轴及x=±1围成的阴影区域.向D中随机投一点,则该点落入E中的概率为( )
如图,设D是图中边长为2的正方形区域,E是函数y=x3的图象与x轴及x=±1围成的阴影区域.向D中随机投一点,则该点落入E中的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
双曲线
-
=1的离心率e=2,则双曲线的渐近线方程为( )
| y2 |
| 16 |
| x2 |
| m |
A、y=±
| ||||
B、y=±
| ||||
| C、y=±2x | ||||
D、y=±
|
已知O是△ABC内一点,若
+2
+3
=
,则△AOC与△ABC的面积的比值为( )
| OA |
| OB |
| OC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 为监测幼儿身体发育状况,某幼儿园对“大班”的100名幼儿的体重做了测量,并根据所得数据画出了频率分布直方图,如图所示.则体重在[18,20](单位kg)的幼儿人数为( )
为监测幼儿身体发育状况,某幼儿园对“大班”的100名幼儿的体重做了测量,并根据所得数据画出了频率分布直方图,如图所示.则体重在[18,20](单位kg)的幼儿人数为( )