题目内容
已知f(x)=2lnx-
,对于任意的x1,x2∈(0,+∞),有|f(x1)-f(x2)|≥m|
-
|,则实数m的取值范围为 .
| 1 |
| x |
| 1 |
| x1 |
| 1 |
| x2 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:利用函数f(x)的单调性,去掉绝对值,构造函数g(x)=f(x)+
,求函数的导数,利用导数和函数单调性之间的关系即可得到结论.
| m |
| x |
解答:
解:函数f(x)=2lnx-
,在x>0时,单调递增,
∵任意的x1,x2∈(0,+∞),
∴当x1=x2时,不等式恒成立,
不妨设任意的x1>x2,则f(x1)>f(x2),
-
<0,
则不等式等价为f(x1)-f(x2)≥-m(
-
),
即f(x1)+
≥f(x2)+
,
令g(x)=f(x)+
,则f(x1)+
≥f(x2)+
,等价为g(x1)≥g(x2),
即函数g(x)=f(x)+
=2lnx-
+
单调递增即可,
即g′(x)≥0在x>0恒成立,
即g′(x)=
+
-
=
≥0,
则m≤2x+1恒成立,
∵x>0,∴2x+1>1,
则m≤1,
故答案为:m≤1.
| 1 |
| x |
∵任意的x1,x2∈(0,+∞),
∴当x1=x2时,不等式恒成立,
不妨设任意的x1>x2,则f(x1)>f(x2),
| 1 |
| x1 |
| 1 |
| x2 |
则不等式等价为f(x1)-f(x2)≥-m(
| 1 |
| x1 |
| 1 |
| x2 |
即f(x1)+
| m |
| x1 |
| m |
| x2 |
令g(x)=f(x)+
| m |
| x |
| m |
| x1 |
| m |
| x2 |
即函数g(x)=f(x)+
| m |
| x |
| 1 |
| x |
| m |
| x |
即g′(x)≥0在x>0恒成立,
即g′(x)=
| 2 |
| x |
| 1 |
| x2 |
| m |
| x2 |
| 2x+1-m |
| x2 |
则m≤2x+1恒成立,
∵x>0,∴2x+1>1,
则m≤1,
故答案为:m≤1.
点评:本题主要考查函数单调性的应用,利用函数单调性和导数之间的关系,构造函数是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
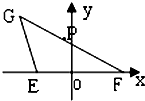 已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,|
已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,|