题目内容
在△ABC中，已知3cscA=cscB•cscC，3sesA=secB•sesC，则cotA的值为 ．
考点：三角函数的化简求值,同角三角函数间的基本关系
专题：三角函数的图像与性质
分析：把正割函数与余割函数化为正弦函数与余弦函数，利用三角形的内角和与诱导公式，化简可得结果．
解答：
解：由3cscA=cscB•cscC，可得：
=sinBsinC…①，
3sesA=secB•sesC，可得
=cosBcosC…②，
②-①可得
-
=cosBcosC-sinBsinC=cos（B+C）=-cosA，
∴4cosA=sinA，
∴cotA=
．
故答案为：
．
| sinA |
| 3 |
3sesA=secB•sesC，可得
| cosA |
| 3 |
②-①可得
| cosA |
| 3 |
| sinA |
| 3 |
∴4cosA=sinA，
∴cotA=
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：本题考查同角三角函数的基本关系式，三角函数的化简求值，考查计算能力．
练习册系列答案
备战中考寒假系列答案
相关题目
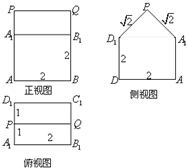某一几何体的三视图如图所示．按照给出的尺寸（单位：cm）：
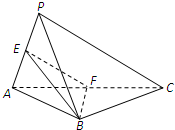如图，在三棱锥P-ABC中，平面ABC⊥平面PAC，AB=BC，E，F分别是PA，AC的中点．求证：