题目内容
20.若函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+(a-1)x+1在区间(1,+∞)上为增函数,则实数a的取值范围是( )| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,2] | D. | (-∞,2) |
分析 求函数的导数,利用函数单调性和导数之间的关系进行求解即可.
解答 解:f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+(a-1)x+1,
f′(x)=x2-ax+(a-1)=[x-(a-1)](x-1),
a-1≤1时,符合题意,
a-1>1时,令f′(x)≥0,解得:x≥a-1或x≤1,
若f(x)在区间(1,+∞)上为增函数,
则a-1≤1,解得:a≤2,
故选:C.
点评 本题主要考查函数单调性的应用,求函数的导数,转化为导数f′(x)≥0恒成立是解决本题的关键.

练习册系列答案
相关题目
15.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左焦点为F,若点F关于直线$y=-\frac{1}{2}x$的对称点P在椭圆C上,则椭圆C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
12.某几何体的三视图如图所示,则该几何体的体积是( )
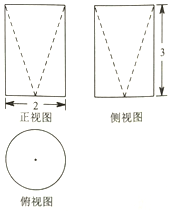

| A. | π | B. | 2π | C. | 3π | D. | 8π |
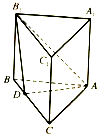 如图,在直三棱柱ABC-A1B1C1中,四边形ABB1A1是边长为$\sqrt{3}$的正方形,BC=3,D为BC上的一点,且平面ADB1⊥平面BCC1B1.
如图,在直三棱柱ABC-A1B1C1中,四边形ABB1A1是边长为$\sqrt{3}$的正方形,BC=3,D为BC上的一点,且平面ADB1⊥平面BCC1B1.