题目内容
8.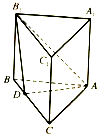 如图,在直三棱柱ABC-A1B1C1中,四边形ABB1A1是边长为$\sqrt{3}$的正方形,BC=3,D为BC上的一点,且平面ADB1⊥平面BCC1B1.
如图,在直三棱柱ABC-A1B1C1中,四边形ABB1A1是边长为$\sqrt{3}$的正方形,BC=3,D为BC上的一点,且平面ADB1⊥平面BCC1B1.(1)求证:AD⊥平面BCC1B1;
(2)若B1D与平面ABC所成角为60°,求三棱锥A1-CB1D的体积.
分析 (1)过B点作BE⊥B1D,垂足为E,则BE⊥平面ADB1,于是BE⊥AD,结合AD⊥BB1得出AD⊥平面BCC1B1;
(2)利用勾股定理计算BD,B1D,AB1,得出AD,CD,代入体积公式计算即可.
解答 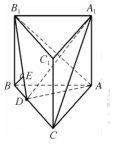 (1)证明:在四边形BB1CC1中,过B点作BE⊥B1D,垂足为E.
(1)证明:在四边形BB1CC1中,过B点作BE⊥B1D,垂足为E.
∵平面AB1D⊥平面BCC1B1,平面AB1D∩平面BCC1B=B1D,BE?平面BCC1B1,
∴BE⊥平面AB1D,又∵AD?平面AB1D,
∴AD⊥BE.
∵BB1⊥平面ABC,AD?平面ABC,
∴AD⊥BB1.又BB1∩BE=B,BB1,BE?平面BCC1B1,
∴AD⊥平面BCC1B1.
(2)解:∵BB1⊥平面ABC,
∴∠B1DB是B1D与平面ABC所成的角,即∠B1DB=60°.
在RtB1BD中,$B{B_1}=\sqrt{3}$,∴BD=1,B1D=2,
又BC=3,∴CD=2.
∴${S_{△C{B_1}D}}=\frac{1}{2}•CD•B{B_1}=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,∵AA1∥BB1,
∴点A1到平面CB1D的距离等于点A到平面CB1D的距离.
由(1)得AD⊥平面BCC1B1,
∵AB1=$\sqrt{2}$AB=$\sqrt{6}$,∴$AD=\sqrt{A{B^2}-B{D^2}}=\sqrt{2}$.
∴${V_{{A_1}-C{B_1}D}}={V_{A-C{B_1}D}}=\frac{1}{3}{S_{△C{B_1}D}}•AD=\frac{1}{3}×\sqrt{3}×\sqrt{2}=\frac{{\sqrt{6}}}{3}$.
点评 本题考查了线面垂直的判定,面面垂直的性质,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
19.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $8+2\sqrt{5}$ | B. | $6+2\sqrt{5}$ | C. | $8+2\sqrt{3}$ | D. | $6+2\sqrt{3}$ |
16. 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )
 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | 8π | B. | 10π | C. | 12π | D. | 8 |
20.若函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+(a-1)x+1在区间(1,+∞)上为增函数,则实数a的取值范围是( )
| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,2] | D. | (-∞,2) |
 如图,四棱锥P-ABCD的一个侧面PAD为等边三角形,且平面PAD⊥平面ABCD,四边形ABCD是平行四边形,AD=2,AB=4,BD=2$\sqrt{3}$
如图,四棱锥P-ABCD的一个侧面PAD为等边三角形,且平面PAD⊥平面ABCD,四边形ABCD是平行四边形,AD=2,AB=4,BD=2$\sqrt{3}$ 四棱锥P-ABCD,侧面PCD为边长为2的正三角形,底面ABCD为对角线互相垂直的等腰梯形,M为AD的中点,$PO=\sqrt{2}$.
四棱锥P-ABCD,侧面PCD为边长为2的正三角形,底面ABCD为对角线互相垂直的等腰梯形,M为AD的中点,$PO=\sqrt{2}$. 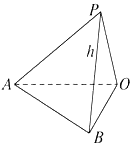 如图所示,在地面上有一旗杆OP,为测得它的高度h,在地面上取一线段AB,
如图所示,在地面上有一旗杆OP,为测得它的高度h,在地面上取一线段AB,