题目内容
9.已知函数f(x)=(x+m)lnx,曲线y=f(x)在x=e(e为自然对数的底数)处得到切线与圆x2+y2=5在点(2,-1)处的切线平行.(1)证明:$f(x)>-\frac{1}{2}$;
(2)若不等式(ax+1)(x-1)<(a+1)lnx在x∈(0,1)上恒成立,求实数a的取值范围.
分析 (1)求出函数的导数,求出m的值,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值即可;
(2)问题转化为(a+1)lnx+$\frac{1}{x}$-ax+a-1>0在x∈(0,1)上恒成立,设h(x)=(a+1)lnx+$\frac{1}{x}$-ax+a-1,x∈(0,+∞),根据函数的单调性求出a的范围即可.
解答 (1)证明:∵f(x)=(x+m)lnx,
∴f′(x)=lnx+$\frac{x+m}{x}$,
易知圆x2+y2=5在点(2,-1)处的切线方程是2x-y=5,
由题意得f′(e)=2,即lne+$\frac{e+m}{e}$=2,解得:m=0,
∴f(x)=xlnx,f′(x)=lnx+1,
令f′(x)=0,解得:x=$\frac{1}{e}$,
x∈(0,$\frac{1}{e}$)时,f′(x)<0,
故f(x)在(0,$\frac{1}{e}$)递减,
x∈($\frac{1}{e}$,+∞)时,f′(x)>0,
故f(x)在($\frac{1}{e}$,+∞)递增,
故f(x)在x=$\frac{1}{e}$处取极小值,也是最小值,最小值是f($\frac{1}{e}$)=-$\frac{1}{e}$,
又-$\frac{1}{e}$>-$\frac{1}{2}$,故f(x)>-$\frac{1}{2}$;
(2)解:若不等式(ax+1)(x-1)<(a+1)lnx在x∈(0,1)上恒成立,
则(a+1)lnx+$\frac{1}{x}$-ax+a-1>0在x∈(0,1)上恒成立,
设h(x)=(a+1)lnx+$\frac{1}{x}$-ax+a-1,x∈(0,+∞),
则h′(x)=$\frac{(1-x)(ax-1)}{{x}^{2}}$,
①a≤0时,h′(x)<0在(0,1)恒成立,
故h(x)在(0,1)递减,又h(1)=0,
故x∈(0,1)时,总有h(x)>0,符合题意;
②a>1时,令h′(x)=0,解得:x=$\frac{1}{a}$或x=1,
易知h(x)在(0,$\frac{1}{a}$)递减,在($\frac{1}{a}$,1)递增,又h(1)=0,
故x∈($\frac{1}{a}$,1)时,总有h(x)<0,不符合题意;
③0<a≤1时,h′(x)<0在(0,1)恒成立,
故h(x)在(0,1)递减,又h(1)=0,
故x∈(0,1)时,总有h(x)>0,符合题意;
综上,a的范围是(-∞,1].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,考查不等式的证明,是一道综合题.

 计算高手系列答案
计算高手系列答案
| A. | $8+2\sqrt{5}$ | B. | $6+2\sqrt{5}$ | C. | $8+2\sqrt{3}$ | D. | $6+2\sqrt{3}$ |
| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,2] | D. | (-∞,2) |
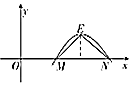 已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的导函数的部分图象如图所示,E是最高点,且△MNE是边长为1的正三角形,那么$f({\frac{1}{3}})$=( )
已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的导函数的部分图象如图所示,E是最高点,且△MNE是边长为1的正三角形,那么$f({\frac{1}{3}})$=( )| A. | $-\frac{{\sqrt{3}}}{2π}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{3}{4π}$ |
| A. | ∅ | B. | {(2,-1)} | C. | {(-1,2),(-2,1)} | D. | {(1,-2),(-1,2),(-2,1)} |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
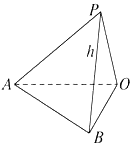 如图所示,在地面上有一旗杆OP,为测得它的高度h,在地面上取一线段AB,
如图所示,在地面上有一旗杆OP,为测得它的高度h,在地面上取一线段AB,