题目内容
5.已知数列{an}的前n项和为Sn,满足Sn=Sn-1+2an-1+1,(n≥2,n∈N*),且a1=3.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设${b_n}={log_2}(\frac{1}{{{a_n}+1}})$,求证:$\frac{1}{{{b_1}{b_2}}}+\frac{1}{{{b_2}{b_3}}}+…+\frac{1}{{{b_n}{b_{n+1}}}}<\frac{1}{2}$.
分析 (Ⅰ)利用已知条件,推出新数列是等比数列,然后求数列{an}的通项公式;
(Ⅱ)化简${b_n}={log_2}(\frac{1}{{{a_n}+1}})$,利用裂项消项法求解数列的和即可证明结果.
解答 (本小题满分12分)
解:(Ⅰ)由题意an=2an-1+1(n≥2,n∈N*)
∴an+1=2(an-1+1)…..(3分)
{an+1}是等比数列,公比为2,首项为:a1+1=4
∴${a_n}+1=4×{2^{n-1}}$…(5分)
∴${a_n}={2^{n+1}}-1$…(6分)
(Ⅱ)证明:${b_n}={log_2}(\frac{1}{{{a_n}+1}})$=$lo{g}_{2}(\frac{1}{{2}^{n+1}-1+1})$=-n-1,
$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{(n+2)(n+1)}$=$\frac{1}{n+1}-\frac{1}{n+2}$,
$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$$+…+\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$$+…+\frac{1}{n+1}-\frac{1}{n+2}$
=$\frac{1}{2}-\frac{1}{n+2}$$<\frac{1}{2}$成立.
点评 本题考查数列的递推关系式的应用,数列求和,考查转化思想以及计算能力.

练习册系列答案
相关题目
15.$\overrightarrow{OA}$=(1,1)在$\overrightarrow{OB}$=(4,3)上的投影为( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{7}{5}$ |
16. 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )
 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | 8π | B. | 10π | C. | 12π | D. | 8 |
20.若函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+(a-1)x+1在区间(1,+∞)上为增函数,则实数a的取值范围是( )
| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,2] | D. | (-∞,2) |
 四棱锥P-ABCD,侧面PCD为边长为2的正三角形,底面ABCD为对角线互相垂直的等腰梯形,M为AD的中点,$PO=\sqrt{2}$.
四棱锥P-ABCD,侧面PCD为边长为2的正三角形,底面ABCD为对角线互相垂直的等腰梯形,M为AD的中点,$PO=\sqrt{2}$. 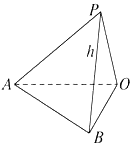 如图所示,在地面上有一旗杆OP,为测得它的高度h,在地面上取一线段AB,
如图所示,在地面上有一旗杆OP,为测得它的高度h,在地面上取一线段AB,