题目内容
10.设x+4y=4(y>0),0<t<z,则$\frac{{4{z^2}}}{|x|}+\frac{{|{x{z^2}}|}}{y}+\frac{12}{{t({z-t})}}$的最小值为24.分析 利用基本不等式求出前两项和第三项的最小值,再利用基本不等式得出三项的和的最小值.
解答 解:∵t(z-t)≤($\frac{z}{2}$)2=$\frac{{z}^{2}}{4}$,∴$\frac{12}{t(z-t)}$≥$\frac{48}{{z}^{2}}$,当且仅当t=z-t即z=2t时取等号,
∵x+4y=4,
∴$\frac{4{z}^{2}}{|x|}$+$\frac{|x{z}^{2}|}{y}$=z2($\frac{x+4y}{|x|}$+$\frac{|x|}{y}$)=z2($\frac{x}{|x|}$+$\frac{4y}{|x|}$+$\frac{|x|}{y}$)≥z2($\frac{x}{|x|}$+4)≥3z2,当且仅当x2=4y2,x<0即x=-4,y=2时取等号,
∴$\frac{{4{z^2}}}{|x|}+\frac{{|{x{z^2}}|}}{y}+\frac{12}{{t({z-t})}}$≥3z2+$\frac{48}{{z}^{2}}$≥2$\sqrt{3×48}$=24.当且仅当3z2=$\frac{48}{{z}^{2}}$即z=2时取等号.
综上,$\frac{{4{z^2}}}{|x|}+\frac{{|{x{z^2}}|}}{y}+\frac{12}{{t({z-t})}}$的最小值为24,当且仅当x=-4,y=2,t=1,z=2时等号成立.
故答案为:24.
点评 本题考查了基本不等式的应用,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
20.若函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+(a-1)x+1在区间(1,+∞)上为增函数,则实数a的取值范围是( )
| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,2] | D. | (-∞,2) |
1.已知集合A={(x,y)|y2<x},B={(x,y)|xy=-2,x∈Z,y∈Z},则A∩B=( )
| A. | ∅ | B. | {(2,-1)} | C. | {(-1,2),(-2,1)} | D. | {(1,-2),(-1,2),(-2,1)} |
19.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一条弦所在的直线方程是x-y+5=0,弦的中点坐标是M(-4,1),则椭圆的离心率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
20.已知函数f(x)=sin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的零点构成一个公差为$\frac{π}{2}$的等差数列,$f(0)=-\frac{{\sqrt{3}}}{2}$,则f(x)的一个单调递增区间是( )
| A. | $(-\frac{5π}{12},\frac{π}{12})$ | B. | $(-\frac{π}{6},\frac{π}{3})$ | C. | $(-\frac{π}{12},\frac{5π}{12})$ | D. | $(\frac{π}{12},\frac{7π}{12})$ |
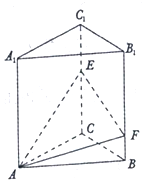 如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.
如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.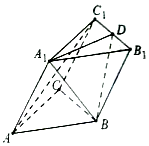 如图,在三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.
如图,在三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.