题目内容

设抛物线y2=12x的焦点为F，经过点P（4，1）的直线l与抛物线相交于A、B两点，且点P恰为AB的中点，则|AF|+|BF|=
 
．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设A（x1，y1），B（x2，y2），由抛物线的定义，得|AF|=x1+3，|BF|=x2+3．又根据中点坐标公式，可得x1+x2=8，代入即可得到|AF|+|BF|的值．
解答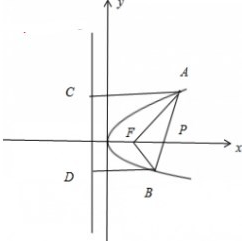： 解：由题意可得F（3，0），
设A（x1，y1），B（x2，y2），抛物线的准线：x=-3，过A、B分别作准线的垂线，垂足分别为C、D，
根据抛物线的定义，得|AF|=|AC|=x1+3，|BF|=|BD|=x2+3，
故|AF|+|BF|=（x1+x2）+6
∵AB中点为P（4，1），
∴
1
2
（x1+x2）=4，可得x1+x2=8
∴|AF|+|BF|=（x1+x2）+6=14
故答案为：14．
点评：本题给出抛物线的弦AB的中点坐标，求A、B两点到焦点距离之和，着重考查了抛物线的定义、标准方程和简单几何性质等知识，属于基础题．
练习册系列答案
相关题目
在直线l：x-y+9=0上任取一点M，过M作以F1（-3，0），F2（3，0）为焦点的椭圆，当M在什么位置时，所作椭圆长轴最短？并求此椭圆方程．
已知定点F1（-1，0），F2（1，0），动点P（x，y），且满足|PF1|，|F1F2|，|PF2|成等差数列．
（Ⅰ） 求点P的轨迹C1的方程；
（Ⅱ） 若曲线C2的方程为（x-t）2+y2=（t2+2t）2（0＜t≤
2
2
），过点A（-2，0）的直线l与曲线C2相切，求直线l被曲线C1截得的线段长的最小值．
4x+3y＜12
x-y＞-1
y≥0
表示的平面区域内整点的个数是
 
．
设变量x，y满足|x|+|y|≤1，则x+2y的取值范围为
 
．
在直角坐标系xOy中，已知A（-1，0），B（0，1），则满足PA2-PB2=4且在圆x2+y2=4上的点P的个数为
 
．
若点M（3，m）在不等式组
x+y-2≥0
2x-y+2≥0
表示的平面区域内，则m的取值范围是
 
．
给出如下命题：
①若“p且q”为假命题，则p，q均为假命题；
②命题“若a＞b，则2a＞2b-1”的否命题为“若a≤b，则2a≤2b-1”；
③命题“?x0∈R，2x0≤0”的否定是“?x∈R，2x＞0”；
④“a≥5”是“?x∈[1，2]，x2-a≤0恒成立”的充要条件．
其中所有正确的命题的序号是
 
．
下列判断错误的是（　　）
A、命题“?x∈R，2x＞0”的否定是“?x0∈R，2x0≤0”
B、命题“若xy=0，则x=0”的否命题为“若xy≠0，则x≠0”
C、函数y=2x-3+1的图象恒过定点A（3，2）
D、“sinα=
1
2
”是“α=
π
6
”的充分不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网