题目内容

在直线l：x-y+9=0上任取一点M，过M作以F1（-3，0），F2（3，0）为焦点的椭圆，当M在什么位置时，所作椭圆长轴最短？并求此椭圆方程．
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：因为|MF1|+|MF2|=2a，即问题转化为在直线上求一点M，使M到F1，F2的距离的和最小，求出F1关于l的对称点F，即求M到F、F2的和最小，FF2的长就是所求的最小值．
解答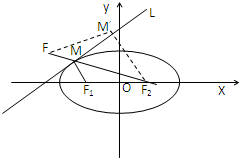： 解：设F1（-3，0）关于l：x-y+9=0的对称点 F（x，y）
则
x-3
2
-
y
2
+9=0
y-0
x+3
=-1
⇒
x=-9
y=6
，即F（-9，6），
连F2F交l于M，点M即为所求．
F2F：y=-
1
2
(x-3)即x+2y-3=0
解方程组
x+2y-3=0
x-y+9=0
⇒
x=-5
y=4
，即M（-5，4）
当点M′取异于M的点时，|FM′|+|M′F2|＞|FF2|．
满足题意的椭圆的长轴2a=|FF2|=
(-9-3)2+62
=6
5

所以a=3
5
，b2=a2-c2=45-9=36
所以椭圆的方程为：
x2
45
+
y2
36
=1．
点评：本题考查直线与椭圆的位置关系，考查学生分析解决问题的能力，问题转化为在直线上求一点M，使M到F1，F2的距离的和最小是解题的关键．
练习册系列答案
相关题目
下面关于f（x）的判断：
①y=f（x-2）与y=f（2-x）的图象关于直线x=2对称；
②若f（x）为偶函数，且f（2+x）=-f（x），则f（x）的图象关于直线x=2对称．
③设函数f（x）=lnx，且x0，x1，x2∈（0，+∞），若x1＜x2，则
1
x2
＞
f(x1)-f(x2)
x1-x2
．
④函数f（x）=lnx，x0，x1，x2∈（0，+∞），存在x0∈（x1，x2），（x1＜x2），使得
1
x0
=
f(x1)-f(x2)
x1-x2
．
⑤设函数f（x）=x2-3x+4，g(x)=
1
2
x2+4lnx+a．对于?x1∈[1，e]，总?x2∈[1，e]，使得f（x1）=g（x2），则实数a的取值范围为[1，
5
4
]．
其中正确的判断是
 
（把你认为正确的判断都填上）
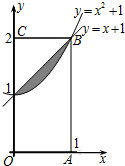如图，在矩形OABC内：记抛物线y=x2+1与直线y=x+1围成的区域为M（图中阴影部分）．随机往矩形OABC内投一点P，则点P落在区域M内的概率是（　　）
A、
1
18
B、
1
12
C、
1
6
D、
1
3
己知命题p：椭圆
x2
10-m
+
y2
m-2
=1，长轴在y轴上．
（Ⅰ）若椭圆焦距为4，求实数m的值；
（Ⅱ）命题q：关于x的不等式x2-2x+m＞0的解集是R；若“p∧q”是假命题，“p∨q”是真命题，求实数m的取值范围．
已知椭圆C：
x2
a2
+
y2
2
=1（a2＞2）的右焦点F到直线x-y+2
2
=0的距离为3．
（1）椭圆C的方程；
（2）是否存在直线l：y=kx+1，使l与椭圆C交于两不同的点M、N，且|FM|=|FN|？若存在，求出k的值，若不存在，请说明理由．
已知抛物线C：y2=2px（p＞0）的准线方程为x=-2．
（1）求此抛物线的方程；
（2）已知点B（-1，0），设直线l：y=kx+b（k≠0）与抛物线C交于不同的两点P（x1，y1），Q（x2，y2），若x轴是∠PBQ的角平分线，证明直线l过定点，并求出该定点坐标．
画出不等式组
x+2y-1≥0
2x+y-5≤0
y≤x+2
所表示的平面区域并求其面积．
已知双曲线C的方程为
y2
a2
-
x2
b2
=1（a＞0，b＞0），离心率e=
5
2
，顶点到渐近线的距离为
2
5
5
．
（1）求双曲线C的方程
（2）求双曲线C的焦点坐标和渐近线方程．
设抛物线y2=12x的焦点为F，经过点P（4，1）的直线l与抛物线相交于A、B两点，且点P恰为AB的中点，则|AF|+|BF|=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网