题目内容
已知函数f（x）=x+lnx和g（x）=x+
．
（1）求f（x）在（1，f（1））处的切线方程．
（2）当a≠0时，求g（x）的单调区间．
| a2 |
| x |
（1）求f（x）在（1，f（1））处的切线方程．
（2）当a≠0时，求g（x）的单调区间．
考点：利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题：综合题,导数的概念及应用
分析：（1）由y=x+1nx，知y′=1+
，由此能求出函数y=x+1nx在点（1，1）处的切线方程；
（2）求导数，分类讨论，利用导数的正负，可得g（x）的单调区间．
| 1 |
| x |
（2）求导数，分类讨论，利用导数的正负，可得g（x）的单调区间．
解答：
解：（1）∵y=x+1nx，
∴y′=1+
，
∴k=y′|x=1=1+1=2，
∴函数y=x+1nx在点（1，1）处的切线方程为y-1=2（x-1），
整理，得2x-y-1=0；
（2）∵g（x）=x+
，
∴g′（x）=
，
a＞0时，由g′（x）＞0可得函数的单调增区间为（-∞，-a），（a，+∞），
由g′（x）＜0可得函数的单调减区间为（-a，0），（0，a）；
a＜0时，由g′（x）＞0可得函数的单调增区间为（-∞，a），（-a，+∞），
由g′（x）＜0可得函数的单调减区间为（a，0），（0，-a）．
∴y′=1+
| 1 |
| x |
∴k=y′|x=1=1+1=2，
∴函数y=x+1nx在点（1，1）处的切线方程为y-1=2（x-1），
整理，得2x-y-1=0；
（2）∵g（x）=x+
| a2 |
| x |
∴g′（x）=
| x2-a2 |
| x2 |
a＞0时，由g′（x）＞0可得函数的单调增区间为（-∞，-a），（a，+∞），
由g′（x）＜0可得函数的单调减区间为（-a，0），（0，a）；
a＜0时，由g′（x）＞0可得函数的单调增区间为（-∞，a），（-a，+∞），
由g′（x）＜0可得函数的单调减区间为（a，0），（0，-a）．
点评：本题考查函数的切线方程的求法，考查函数的单调区间，考查分类讨论的数学思想，正确求导是关键．
练习册系列答案
春雨教育同步作文系列答案
相关题目
已知集合A={x|x2-3x＜0}，B={x|log3（x-1）＜1}，则下列结论中正确的是（ ）
| A、2∈A∩B且1∈A∪B |
| B、2∈A∩B且1∉A∪B |
| C、2∉A∩B且1∈A∪B |
| D、2∉A∩B且1∉A∪B |
如图，△ABC内接于圆O，∠A的平分线交BC于点D，交外接圆于点E，求证：AD2=AB•AC-BD•DC．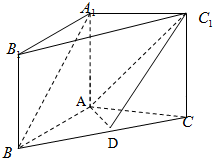
在三棱柱A1B1C1-ABC中，A1A⊥平面ABC，A1A=AB=AC=2，BC=2