题目内容
已知集合A={x|x2-3x<0},B={x|log3(x-1)<1},则下列结论中正确的是( )
| A、2∈A∩B且1∈A∪B |
| B、2∈A∩B且1∉A∪B |
| C、2∉A∩B且1∈A∪B |
| D、2∉A∩B且1∉A∪B |
考点:元素与集合关系的判断
专题:集合
分析:解二次不等式求出集合A,解对数不等式求出集合B,进而求出A∩B和A∪B,进而判断2,1两个元素与集合A∩B和A∪B的关系,得到答案.
解答:
解:集合A={x|x2-3x<0}=(0,3),
B={x|log3(x-1)<1}={x|0<x-1<3}=(1,4),
故A∩B=(1,3),A∪B=(0,4),
故2∈A∩B且1∈A∪B,
故选:A.
B={x|log3(x-1)<1}={x|0<x-1<3}=(1,4),
故A∩B=(1,3),A∪B=(0,4),
故2∈A∩B且1∈A∪B,
故选:A.
点评:本题考查的知识点是元素与集合关系的判断,其中解不等式求出集合A,B是解答的关键.

练习册系列答案
相关题目
能够把圆O:x2+y2=r2(r>0)的周长和面积同时分为相等的两部分的函数称之为圆O的“和谐函数”,下列函数不是圆O的“和谐函数”的是( )
| A、f(x)=4x3+x | ||
B、f(x)=ln
| ||
C、f(x)=tan
| ||
| D、f(x)=ex+e-x |
复数
在复平面内对应的点位于( )
| 1-i |
| 2+3i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知A(1,0),点B在曲线G:y=ln(x+1)上,若线段AB与曲线M:y=
相交且交点恰为线段AB的中点,则称B为曲线G关于曲线M的一个关联点.记曲线G关于曲线M的关联点的个数为a,则( )
| 1 |
| x |
| A、a=0 | B、a=1 |
| C、a=2 | D、a>2 |
i是虚数单位,复数(
)2表示的点落在哪个象限( )
| 3-i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知n∈N,常数p,q均大于1,且都不等于2,则
=( )
| lim |
| n→∞ |
| pn+1-qn |
| pn+2-2qn+1 |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
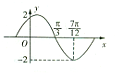 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤