题目内容
设实数a，b，定义运算“⊕”：a?b=
，设函数f（x）=（2-x）?（x+1），x∈R．则关于x的方程f（x）=x的解集为 ．
|
考点：根的存在性及根的个数判断
专题：计算题,新定义,函数的性质及应用,不等式的解法及应用
分析：由新定义可得函数f（x）=（2-x）?（x+1）=
，对x讨论，即可解得f（x）=x的解集．
|
解答：
解：函数f（x）=（2-x）?（x+1），
=
，
则有f（x）=x，即为2-x=x（x≥0）或x+1=x（x＜0），
解得x=1．
故答案为：{1}．
=
|
则有f（x）=x，即为2-x=x（x≥0）或x+1=x（x＜0），
解得x=1．
故答案为：{1}．
点评：本题考查新定义及运用，考查不等式的解法，属于基础题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
如果一个数列{an}满足an+1+an=h（h为常数，n∈N*），则称数列{an}为等和数列，h为公和，Sn是其前n项的和，已知等和数列{an}中，a1=1，h=-3，则S2015等（ ）
| A、3020 | B、3021 |
| C、-3020 | D、-3021 |
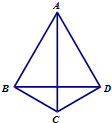如图，将两个全等的30°的直角三角形ABC和直角三角形ADC拼在一起组成平面四边形ABCD，若| DB |
| DA |
| DC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知f（x6）=log2x，则f（8）=（ ）
A、
| ||
| B、8 | ||
| C、18 | ||
D、
|
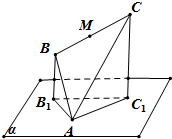如图，边长为4的正△ABC顶点A在平面α上，B，C在平面α的同侧，且点C到平面α的距离是点B到平面α的距离的