题目内容
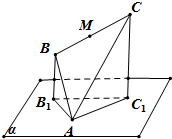如图，边长为4的正△ABC顶点A在平面α上，B，C在平面α的同侧，且点C到平面α的距离是点B到平面α的距离的| 3 |
| 2 |
考点：点、线、面间的距离计算
专题：计算题,空间位置关系与距离
分析：设出B，C到面的距离，则M到平面α的距离为两者和的一半，确定a=
，即可求出M到平面α的距离的取值范围．
4
| ||
| 3 |
解答：
解：设B到平面α距离为a，则点C到平面α的距离为
a，M到平面α距离为h=
a，
射影三角形两直角边的平方分别4-a2，4-
a2，
设线段BC射影长为c，则4-a2+4-
a2=c2，（1）
又线段AM射影长为
，所以（
）2+
a2=12，（2）
由（1）（2）联立解得a=
，
∴h=
，
故答案为：
．
| 3 |
| 2 |
| 5 |
| 4 |
射影三角形两直角边的平方分别4-a2，4-
| 9 |
| 4 |
设线段BC射影长为c，则4-a2+4-
| 9 |
| 4 |
又线段AM射影长为
| c |
| 2 |
| c |
| 2 |
| 25 |
| 16 |
由（1）（2）联立解得a=
4
| ||
| 3 |
∴h=
5
| ||
| 3 |
故答案为：
5
| ||
| 3 |
点评：本题考查M到平面α的距离，考查学生分析解决问题的能力，确定a=
是关键．
4
| ||
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
将函数y=cos(
π-ωx)(ω＞0)的图象向左平移
个单位后，得到函数y=sin（2x+φ）的图象，则函数y=sin（2x+φ）的一个对称中心为（ ）
| 3 |
| 2 |
| π |
| 3 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
方程lnx=2-x的根所在区间是（ ）
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
函数f（x）=-x3-3x+5的零点所在的区间为（ ）
| A、（1，2） |
| B、（-2，0） |
| C、（0，1） |
| D、（-2，1） |