题目内容
计算
(1)2x
(-3x-
y
);
(2)(a
+a-
)2;
(3)log336-log34;
(4)log2
•log3
•log5
.
(1)2x
| 1 | ||
|
| 1 | ||
|
| 3 |
(2)(a
| 1 |
| 2 |
| 1 |
| 2 |
(3)log336-log34;
(4)log2
| 1 |
| 125 |
| 1 |
| 32 |
| 1 |
| 3 |
考点:对数的运算性质,根式与分数指数幂的互化及其化简运算
专题:函数的性质及应用
分析:(1)(2)利用有理指数幂的运算法则求解即可.
(3)利用对数的运算法则求解即可.
(4)利用对数的换底公式化简求解即可.
(3)利用对数的运算法则求解即可.
(4)利用对数的换底公式化简求解即可.
解答:
解:(1)2x
(-3x-
y
)
=-6x
-
y
=-6y
;
(2)(a
+a-
)2
=a+a-1+2;
(3)log336-log34
=log39
=2;
(4)log2
•log3
•log5
=
×
×
=-15.
| 1 | ||
|
| 1 | ||
|
| 3 |
=-6x
| 1 | ||
|
| 1 | ||
|
| 3 |
=-6y
| 3 |
(2)(a
| 1 |
| 2 |
| 1 |
| 2 |
=a+a-1+2;
(3)log336-log34
=log39
=2;
(4)log2
| 1 |
| 125 |
| 1 |
| 32 |
| 1 |
| 3 |
=
| -3lg5 |
| lg2 |
| -5lg2 |
| lg3 |
| -lg3 |
| lg5 |
=-15.
点评:本题考查有理指数幂的运算法则、对数的运算法则以及对数的换底公式的应用,基本知识与方法的考查.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
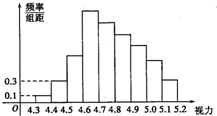 为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,视力在4.6到5.0之间的学生数为a,则a的值为( )
为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,视力在4.6到5.0之间的学生数为a,则a的值为( )| A、136 | B、146 |
| C、156 | D、166 |
将函数y=cos(
π-ωx)(ω>0)的图象向左平移
个单位后,得到函数y=sin(2x+φ)的图象,则函数y=sin(2x+φ)的一个对称中心为( )
| 3 |
| 2 |
| π |
| 3 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|