题目内容
定义在非零实数集上的函数f（xy）=f（x）+f（y），则函数f（x）的奇偶性是 ．
考点：函数奇偶性的判断
专题：计算题,函数的性质及应用
分析：令x=y=1，利用恒等式f（xy）=f（x）+f（y）可求f（1），令x=y=-1，求f（-1），令y=-1，代入f（xy）=f（x）+f（y），结合（1）的结论即可证得f（-x）=f（x）．
解答：
解：令x=y=1，由f（xy）=f（x）+f（y）得f（1）=0
令x=y=-1，则f（0）=2f（-1）
∴f（-1）=0，
又令y=-1，则f（-x）=f（x）+f（-1）=f（x），所以f（x）为偶函数．
故答案为：偶函数．
令x=y=-1，则f（0）=2f（-1）
∴f（-1）=0，
又令y=-1，则f（-x）=f（x）+f（-1）=f（x），所以f（x）为偶函数．
故答案为：偶函数．
点评：本题主要考查了利用赋值求解抽象函数的函数值，及奇偶性的判断与证明，比较基础．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
相关题目
已知f（x）=x2+bx+c，且f（1）=f（3）=0，则f（x）的单调递减区间为（ ）
| A、（-∞，1）或（3 ，+∞） |
| B、（1，3） |
| C、（-∞，2） |
| D、（2，+∞） |
若a=3tan60°，b=log
cos60°，c=log2tan30°，则（ ）
| 1 |
| 3 |
| A、a＞b＞c |
| B、b＞c＞a |
| C、c＞b＞a |
| D、b＞a＞c |
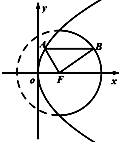已知△ABF，点F（2，0），点A，B分别在图中抛物线y2=8x及圆（x-2）2+y2=16的实线部分上运动，且AB总是平行于x轴，则△ABF的周长的取值范围是
某几何体的三视图如图所示，图中的三个视图均为边长为2的正方形，则该几何体的体积为（ ）A、
| ||
B、
| ||
| C、4 | ||
| D、6 |
