题目内容
已知椭圆C:
+
=1,(a>b>0)的离心率等于
,点P(2,
)在椭圆上.
(1)求椭圆C的方程;
(2)设椭圆C的左右顶点分别为A,B,过点Q(2,0)的动直线l与椭圆C相交于M,N两点,是否存在定直线l′:x=t,使得l′与AN的交点G总在直线BM上?若存在,求出一个满足条件的t值;若不存在,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
(1)求椭圆C的方程;
(2)设椭圆C的左右顶点分别为A,B,过点Q(2,0)的动直线l与椭圆C相交于M,N两点,是否存在定直线l′:x=t,使得l′与AN的交点G总在直线BM上?若存在,求出一个满足条件的t值;若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可得:
,解得即可.
(2)当l⊥x轴时,M(2,
),N(2,-
),联立直线AN、BM的方程可得G(8,-2
).猜测常数t=8.
即存在定直线l′:x=t,使得l′与AN的交点G总在直线BM上.当直线l的斜率存在时,设l的方程为:y=k(x-2),M(x1,y1),N(x2,y2),G(8,t).把直线方程与椭圆方程联立可得根与系数的关系,由于
=(12,t),
=(x2+4,y2),利用三点共线可得t(x2+4)-12y2=0,只要证明三点B,M,G共线即可.利用向量的坐标运算及其根与系数的关系即可证明.
|
(2)当l⊥x轴时,M(2,
| 3 |
| 3 |
| 3 |
即存在定直线l′:x=t,使得l′与AN的交点G总在直线BM上.当直线l的斜率存在时,设l的方程为:y=k(x-2),M(x1,y1),N(x2,y2),G(8,t).把直线方程与椭圆方程联立可得根与系数的关系,由于
| AG |
| AN |
解答:
解:(1)∵椭圆C:
+
=1,(a>b>0)的离心率等于
,点P(2,
)在椭圆上.
∴
,解得a2=16,b2=4,c=2
.∴椭圆C的方程为
+
=1.
(2)当l⊥x轴时,M(2,
),N(2,-
),直线AN、BM的方程分别为y=
(x+4),y=
(x-4).
分别化为:
x+6y+4
=0,
x+2y-4
=0.联立解得G(8,-2
).猜测常数t=8.
即存在定直线l′:x=t,使得l′与AN的交点G总在直线BM上.
证明:当直线l的斜率存在时,设l的方程为:y=k(x-2),M(x1,y1),N(x2,y2),G(8,t).
联立
,化为(1+4k2)x2-16k2x+16k2-16=0.
∴x1+x2=
,x1x2=
.
∵
=(12,t),
=(x2+4,y2),三点A,N,G共线.
∴t(x2+4)-12y2=0,∴t=
=
由于
=(4,t),
=(x1-4,y1),要证明三点B,M,G共线.
即证明t(x1-4)-4y1=0.即证明
-4k(x1-2)=0,
而3(x2-2)(x1-4)-(x1-2)(x2+4)=2x1x2-10(x1+x2)+32=
-
+32=0,
∴
-4k(x1-2)=0成立.
∴存在定直线l′:x=8,使得l′与AN的交点G总在直线BM上.
综上可知:存在定直线l′:x=8,使得l′与AN的交点G总在直线BM上.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
∴
|
| 3 |
| x2 |
| 16 |
| y2 |
| 4 |
(2)当l⊥x轴时,M(2,
| 3 |
| 3 |
| ||
| -6 |
| ||
| 2-4 |
分别化为:
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
即存在定直线l′:x=t,使得l′与AN的交点G总在直线BM上.
证明:当直线l的斜率存在时,设l的方程为:y=k(x-2),M(x1,y1),N(x2,y2),G(8,t).
联立
|
∴x1+x2=
| 16k2 |
| 1+4k2 |
| 16k2-16 |
| 1+4k2 |
∵
| AG |
| AN |
∴t(x2+4)-12y2=0,∴t=
| 12y2 |
| x2+4 |
| 12k(x2-2) |
| x2+4 |
由于
| BG |
| BM |
即证明t(x1-4)-4y1=0.即证明
| 12k(x2-2)(x1-4) |
| x2+4 |
而3(x2-2)(x1-4)-(x1-2)(x2+4)=2x1x2-10(x1+x2)+32=
| 32(k2-1) |
| 1+4k2 |
| 160k2 |
| 1+4k2 |
∴
| 12k(x2-2)(x1-4) |
| x2+4 |
∴存在定直线l′:x=8,使得l′与AN的交点G总在直线BM上.
综上可知:存在定直线l′:x=8,使得l′与AN的交点G总在直线BM上.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量的坐标运算、向量共线定理,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
命题p:x(x-3)=0,命题q:x=3,则命题p是命题q的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
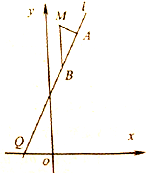 如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=
如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=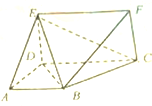 如图所示,直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=1,CD=2.
如图所示,直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=1,CD=2.