题目内容
若a=3tan60°,b=log
cos60°,c=log2tan30°,则( )
| 1 |
| 3 |
| A、a>b>c |
| B、b>c>a |
| C、c>b>a |
| D、b>a>c |
考点:对数值大小的比较
专题:函数的性质及应用
分析:根据三角函数以及指数函数和对数函数的性质即可得到结论.
解答:
解:tan60°=
,cos60°=
,tan30°=
,
则a=3tan60°=3
>3,
b=log
cos60°=log
∈(0,1),c=log2tan30°=log2
<0,
则a>b>c,
故选:A
| 3 |
| 1 |
| 2 |
| ||
| 3 |
则a=3tan60°=3
| 3 |
b=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
则a>b>c,
故选:A
点评:本题主要考查函数值的大小比较,根据指数函数和对数函数的性质是解决本题的关键.

练习册系列答案
相关题目
若函数f(x)=
x2-ax+lnx存在垂直于y轴的切线,则实数a的取值范围是( )
| 1 |
| 2 |
| A、(-∞,-2]∪[2,+∞) |
| B、(-∞,-2)∪(2,+∞) |
| C、[2,+∞) |
| D、(2,+∞) |
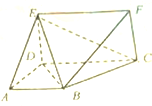 如图所示,直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=1,CD=2.
如图所示,直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=1,CD=2.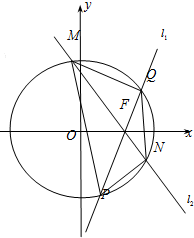 已知椭圆
已知椭圆