Question

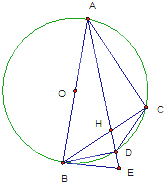
如图，⊙O的直径AB，BE为圆0的切线，点C为⊙O 上不同于A、B的一点，AD为∠BAC的平分线，且分别与BC 交于H，与⊙O交于D，与BE交于E，连结BD、CD．
（1）求证：∠DBE=∠DBC
（2）若HE=2a，求ED．

Answer 1

考点：与圆有关的比例线段

专题：直线与圆

分析：（1）由已知得∠BAD=∠CAD=∠DBC，∠DBE=∠BAE，由此能证明∠DBE=∠DBC．
（2）由⊙O的直径AB，∠ADB=90°，由此能求出ED．

解答： （1）证明：∵⊙O的直径AB，BE为圆0的切线，点C为⊙O 上不同于A、B的一点，AD为∠BAC的平分线，
且分别与BC 交于H，与⊙O交于D，与BE交于E，连结BD、CD，
∴∠BAD=∠CAD=∠DBC，∠DBE=∠BAE，
∴∠DBE=∠DBC．
（2）解：∵⊙O的直径AB
∴∠ADB=90°，
又由（1）得∠DBE=∠DBH，
∵HE=2a，
∴ED=a．

点评：本题考查两角相等的求法，考查线段长的求法，解题时要认真审题，注意圆的性质的合理运用．