题目内容
若xlog23=1,则3x+3-x的值为 .
考点:对数的运算性质,有理数指数幂的化简求值
专题:函数的性质及应用
分析:由已知得x=log32,从而3x+3-x=3 log32+3 -log32,由此能求出结果.
解答:
解:∵xlog23=1,∴x=log32,
∴3x+3-x=3 log32+3 -log32
=2+
=
.
故答案为:
.
∴3x+3-x=3 log32+3 -log32
=2+
| 1 |
| 2 |
=
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意对数性质的合理运用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
[x]表示不超过x的最大整数,函数f(x)=|x|-[x]
①f(x)的定义域为R;
②f(x)的值域为(0,1];
③f(x)是偶函数;
④f(x)不是周期函数;
⑤f(x)的单调增区间为(k,k+1)(k∈N).
上面的结论正确的个数是( )
①f(x)的定义域为R;
②f(x)的值域为(0,1];
③f(x)是偶函数;
④f(x)不是周期函数;
⑤f(x)的单调增区间为(k,k+1)(k∈N).
上面的结论正确的个数是( )
| A、3 | B、2 | C、1 | D、0 |
若函数f(x)=
x2-ax+lnx存在垂直于y轴的切线,则实数a的取值范围是( )
| 1 |
| 2 |
| A、(-∞,-2]∪[2,+∞) |
| B、(-∞,-2)∪(2,+∞) |
| C、[2,+∞) |
| D、(2,+∞) |
命题p:x(x-3)=0,命题q:x=3,则命题p是命题q的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
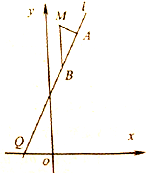 如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=
如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=