题目内容
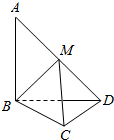 在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:空间角
分析:(1)利用面面垂直的性质定理即可得出;
(2)建立如图所示的空间直角坐标系.设直线AD与平面MBC所成角为θ,利用线面角的计算公式sinθ=|cos<
,
>|=
即可得出.
(2)建立如图所示的空间直角坐标系.设直线AD与平面MBC所成角为θ,利用线面角的计算公式sinθ=|cos<
| n |
| AD |
|
| ||||
|
|
解答:
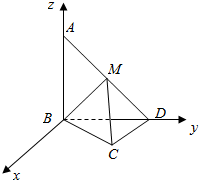 (1)证明:∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB?平面ABD,AB⊥BD,
(1)证明:∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB?平面ABD,AB⊥BD,
∴AB⊥平面BCD,又CD?平面BCD,∴AB⊥CD.
(2)解:建立如图所示的空间直角坐标系.
∵AB=BD=CD=1,AB⊥BD,CD⊥BD,
∴B(0,0,0),C(1,1,0),A(0,0,1),D(0,1,0),M(0,
,
).
∴
=(0,1,-1),
=(1,1,0),
=(0,
,
).
设平面BCM的法向量
=(x,y,z),则
,
令y=-1,则x=1,z=1.
∴
=(1,-1,1).
设直线AD与平面MBC所成角为θ.
则sinθ=|cos<
,
>|=
=
=
.
 (1)证明:∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB?平面ABD,AB⊥BD,
(1)证明:∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB?平面ABD,AB⊥BD,∴AB⊥平面BCD,又CD?平面BCD,∴AB⊥CD.
(2)解:建立如图所示的空间直角坐标系.
∵AB=BD=CD=1,AB⊥BD,CD⊥BD,
∴B(0,0,0),C(1,1,0),A(0,0,1),D(0,1,0),M(0,
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AD |
| BC |
| BM |
| 1 |
| 2 |
| 1 |
| 2 |
设平面BCM的法向量
| n |
|
令y=-1,则x=1,z=1.
∴
| n |
设直线AD与平面MBC所成角为θ.
则sinθ=|cos<
| n |
| AD |
|
| ||||
|
|
| 2 | ||||
|
| ||
| 3 |
点评:本题综合考查了面面垂直的性质定理、线面角的计算公式sinθ=|cos<
,
>|=
,考查了推理能力和空间想象能力,属于中档题.
| n |
| AD |
|
| ||||
|
|

练习册系列答案
相关题目
 为了了解范县一中2500名男生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图,据此估计该校高中男生体重在70~78kg的人数为( )
为了了解范县一中2500名男生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图,据此估计该校高中男生体重在70~78kg的人数为( )| A、300 | B、160 |
| C、80 | D、60 |
已知点集P={(x,y)|x,y∈{1,2,3}},从集合P中任取一点,纵横坐标和为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2)
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2)