题目内容
△ABC中，∠ABC=90°，若BD⊥AC且BD交AC于点D，丨
丨=
，则
•
= ．
| BD |
| 3 |
| BD |
| BC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用两个向量的加减法的法则，以及其几何意义，把要求的式子化为AB2-AD2，再利用勾股定理结合条件求得结果．
解答：
解：由题意可得
•
=（
-
）•（
-
）
=
•
-
•
-
•
+AB2=|
|•|
|-|
|•|
|cosA-|
|•|
|•cosA-|
|2
=|
|•|
|-|
|2-|
|•|
|-|
|2=AB2-AD2=BD2=3，
故答案为：3．
| BD |
| BC |
| AD |
| AB |
| AC |
| AB |
=
| AD |
| AC |
| AD |
| AB |
| AB |
| AC |
. |
| AD |
| AC |
| AD |
| AB |
| AB |
| AC |
| AB |
=|
. |
| AD |
| AC |
| AD |
| AB |
| AD |
| AB |
故答案为：3．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，向量的模的定义和求法，属于中档题．
练习册系列答案
相关题目
若不等式lg
≥（x-1）lg3对任意x∈（-∞，1）恒成立，则a的取值范围是（ ）
| 1+2x+(1-a)3x |
| 3 |
| A、（-∞，0] |
| B、[1，+∞） |
| C、[0，+∞） |
| D、（-∞，1] |
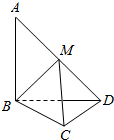在平面四边形ABCD中，AB=BD=CD=1，AB⊥BD，CD⊥BD，将△ABD沿BD折起，使得平面ABD⊥平面BCD，如图．
设b、c分别是先后抛掷一枚骰子得到的点数，则函数f（x）=x2+bx+c有零点的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|