��Ŀ����
������������P����a1��b1������a2��b2����������an��bn������T1��P��=a1+b1��Tk��P��=bk+max{Tk-1��P����a1+a2+��+ak}��2��k��n��������max{Tk-1��P����a1+a2+��+ak}��ʾTk-1��P����a1+a2+��+ak����������������
��������������P����2��5������4��1������T1��P����T2��P����ֵ��
����mΪa��b��c��d�ĸ�������С�������������������ԣ�a��b������c��d����ɵ���������P����a��b������c��d����P�䣺��c��d������a��b�����Էֱ��m=a��m=d��������Ƚ�T2��P����T2��P�䣩�Ĵ�С��
��������������ԣ�11��8������5��2������16��11������11��11������4��6����ɵ��������������У�д��һ����������PʹT5��P����С����д��T5��P����ֵ��ֻ��д�����ۣ���
��������������P����2��5������4��1������T1��P����T2��P����ֵ��
����mΪa��b��c��d�ĸ�������С�������������������ԣ�a��b������c��d����ɵ���������P����a��b������c��d����P�䣺��c��d������a��b�����Էֱ��m=a��m=d��������Ƚ�T2��P����T2��P�䣩�Ĵ�С��
��������������ԣ�11��8������5��2������16��11������11��11������4��6����ɵ��������������У�д��һ����������PʹT5��P����С����д��T5��P����ֵ��ֻ��д�����ۣ���
���㣺���������ۺϷ�
ר�⣺�¶���,������
��������������T1��P��=a1+b1��Tk��P��=bk+max{Tk-1��P����a1+a2+��+ak}��2��k��n��������T1��P����T2��P����ֵ��
����T2��P��=max{a+b+d��a+c+d}��T2��P�䣩=max{c+d+b��c+a+b}���������ۣ������¶��壬�ɱȽ�T2��P����T2��P�䣩�Ĵ�С��
�������¶��壬�ɵý��ۣ�
����T2��P��=max{a+b+d��a+c+d}��T2��P�䣩=max{c+d+b��c+a+b}���������ۣ������¶��壬�ɱȽ�T2��P����T2��P�䣩�Ĵ�С��
�������¶��壬�ɵý��ۣ�
���
�⣺����T1��P��=2+5=7��T2��P��=1+max{T1��P����2+4}=1+max{7��6}=8��
����T2��P��=max{a+b+d��a+c+d}��T2��P�䣩=max{c+d+b��c+a+b}��
��m=aʱ��T2��P�䣩=max{c+d+b��c+a+b}=c+d+b��
��a+b+d��c+d+b����a+c+d��c+b+d����T2��P����T2��P�䣩��
��m=dʱ��T2��P�䣩=max{c+d+b��c+a+b}=c+a+b��
��a+b+d��c+a+b����a+c+d��c+a+d����T2��P����T2��P�䣩��
������m=a��m=d��T2��P����T2��P�䣩��
�������ԣ�4��6������11��11������16��11������11��8������5��2����T5��P����С��
T1��P��=10��T2��P��=26��T3��P��42��T4��P��=50��T5��P��=52��
����T2��P��=max{a+b+d��a+c+d}��T2��P�䣩=max{c+d+b��c+a+b}��
��m=aʱ��T2��P�䣩=max{c+d+b��c+a+b}=c+d+b��
��a+b+d��c+d+b����a+c+d��c+b+d����T2��P����T2��P�䣩��
��m=dʱ��T2��P�䣩=max{c+d+b��c+a+b}=c+a+b��
��a+b+d��c+a+b����a+c+d��c+a+d����T2��P����T2��P�䣩��
������m=a��m=d��T2��P����T2��P�䣩��
�������ԣ�4��6������11��11������16��11������11��8������5��2����T5��P����С��
T1��P��=10��T2��P��=26��T3��P��42��T4��P��=50��T5��P��=52��
���������⿼���¶��壬����ѧ����������������������ȷ�����������¶����ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
��֪���н���1������Ϊ�����Һ�����m�������n������m��3��n��3�������Һ��������ȡi��i=1��2�����������У�
��a������i������к��к���ĸ�����Ϊ��i��i=1��2����
��b������i����Ӽ���ȡ1�����Ǻ���ĸ��ʼ�Ϊpi��i=1��2����
������
��a������i������к��к���ĸ�����Ϊ��i��i=1��2����
��b������i����Ӽ���ȡ1�����Ǻ���ĸ��ʼ�Ϊpi��i=1��2����
������
| A��p1��p2��E����1����E����2�� |
| B��p1��p2��E����1����E����2�� |
| C��p1��p2��E����1����E����2�� |
| D��p1��p2��E����1����E����2�� |
��ʵ��x��y���㲻��ʽ��
����x��yΪ��������3x+4y�����ֵ�ǣ�������
|
| A��26 | B��25 | C��23 | D��22 |
 ��ͼ������A-BCD�У�AB��ƽ��BCD��CD��BD��
��ͼ������A-BCD�У�AB��ƽ��BCD��CD��BD��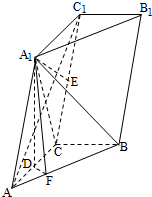 ��ͼ��������ABC-A1B1C1�У���A1��ƽ��ABC�ڵ���ӰD��AC�ϣ���ACB=90�㣬BC=1��AC=CC1=2��
��ͼ��������ABC-A1B1C1�У���A1��ƽ��ABC�ڵ���ӰD��AC�ϣ���ACB=90�㣬BC=1��AC=CC1=2��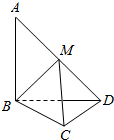 ��ƽ���ı���ABCD�У�AB=BD=CD=1��AB��BD��CD��BD������ABD��BD����ʹ��ƽ��ABD��ƽ��BCD����ͼ��
��ƽ���ı���ABCD�У�AB=BD=CD=1��AB��BD��CD��BD������ABD��BD����ʹ��ƽ��ABD��ƽ��BCD����ͼ�� �Ķ���ͼ��ʾ�ij����ͼ���ش��������⣺
�Ķ���ͼ��ʾ�ij����ͼ���ش��������⣺