题目内容
已知点集P={(x,y)|x,y∈{1,2,3}},从集合P中任取一点,纵横坐标和为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:列举出总的基本事件共9个,符合条件的基本事件共5个,可得所求概率.
解答:
解:从集合P={(x,y)|x,y∈{1,2,3}}中任取一点的基本事件:
(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3)共9个,
其中纵横坐标和为偶数的基本事件为:(1,1)(1,3)(2,2)(3,1)(3,3)共5个,
故纵横坐标和为偶数的概率P=
故选:D
(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3)共9个,
其中纵横坐标和为偶数的基本事件为:(1,1)(1,3)(2,2)(3,1)(3,3)共5个,
故纵横坐标和为偶数的概率P=
| 5 |
| 9 |
故选:D
点评:本题考查古典概型及其概率公式,列举是解决问题的关键,属基础题.

练习册系列答案
相关题目
设b、c分别是先后抛掷一枚骰子得到的点数,则函数f(x)=x2+bx+c有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知六张卡片中,三张红色,三张黑色,它们分别标有数字2,3,4,打乱后分给甲,乙,丙三人,每人两张,若两张卡片所标数字相同称为“一对”卡片,则三人中至少有一人拿到“一对”卡片的分法数为( )
| A、18 | B、24 | C、42 | D、48 |
设实数x,y满足不等式组
,若x,y为整数,则3x+4y的最大值是( )
|
| A、26 | B、25 | C、23 | D、22 |
设函数f(x)=x3-4x+a(a>0),若f(x)的三个零点分别为x1,x2,x3,且x1<x2<x3,则( )
| A、x1>-2 | ||
B、x12+x22<
| ||
| C、x3>2 | ||
D、x22+x32<
|
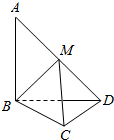 在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.