题目内容
为了了解范县一中2500名男生的身体发育情况，抽查了该校100名高中男生的体重情况，根据所得数据画出样本的频率分布直方图，据此估计该校高中男生体重在70～78kg的人数为（ ）| A、300 | B、160 |
| C、80 | D、60 |
考点：频率分布直方图
专题：概率与统计
分析：根据频率分布直方图，求出体重在70～78kg的频率，再求出对应的人数是多少．
解答：
解：根据频率分布直方图，得；
体重在70～78kg的频率是
1-（0.02+0.07+0.09+0.04）×4=0.12
∴体重在70～78kg的人数为2500×0.12=300．
故选：A．
体重在70～78kg的频率是
1-（0.02+0.07+0.09+0.04）×4=0.12
∴体重在70～78kg的人数为2500×0.12=300．
故选：A．
点评：本题考查了频率分布直方图的应用问题，解题时应根据频率分布直方图，得出频率，再由频率、频数与样本容量的关系，进行计算，即可得出正确的答案，是基础题．
练习册系列答案
相关题目
复数z=
的虚部是（ ）
| 1-2i |
| i |
| A、1 | B、-1 | C、i | D、-i |
若复数
+
（i为虚数单位）的实部与虚部互为相反数，则实数a的值为（ ）
| a |
| 1-i |
| 1-i |
| 2 |
| A、2 | B、1 | C、-1 | D、0 |
已知甲盒中仅有1个球且为红球，乙盒中有m个红球和n个蓝球（m≥3，n≥3），从乙盒中随机抽取i（i=1，2）个球放入甲盒中．
（a）放入i个球后，甲盒中含有红球的个数记为ξi（i=1，2）；
（b）放入i个球后，从甲盒中取1个球是红球的概率记为pi（i=1，2）．
则（ ）
（a）放入i个球后，甲盒中含有红球的个数记为ξi（i=1，2）；
（b）放入i个球后，从甲盒中取1个球是红球的概率记为pi（i=1，2）．
则（ ）
| A、p1＞p2，E（ξ1）＜E（ξ2） |
| B、p1＜p2，E（ξ1）＞E（ξ2） |
| C、p1＞p2，E（ξ1）＞E（ξ2） |
| D、p1＜p2，E（ξ1）＜E（ξ2） |
设点（a，b）是区域
内的随机点，函数f（x）=ax2-4bx+1在区间[1，+∞）上是增函数的概率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
若不等式lg
≥（x-1）lg3对任意x∈（-∞，1）恒成立，则a的取值范围是（ ）
| 1+2x+(1-a)3x |
| 3 |
| A、（-∞，0] |
| B、[1，+∞） |
| C、[0，+∞） |
| D、（-∞，1] |
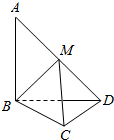在平面四边形ABCD中，AB=BD=CD=1，AB⊥BD，CD⊥BD，将△ABD沿BD折起，使得平面ABD⊥平面BCD，如图．