题目内容
11.学校的校园活动中有这样一个项目.甲箱子中装有大小相同、质地均匀的4个白球,3个黑球.乙箱子中装有大小相同、质地均匀的3个白球,2个黑球.(1)从两个箱子中分别摸出1个球,如果它们都是白球则获胜,有人认为,这两个箱子里装的白球比黑球多,所以获胜的概率大于0.5,你认为呢?并说明理由;
(2)如果从甲箱子中不放回地随机取出4个球.求取到的白球数的分布列和期望;
(3)如果从甲箱子中随机取出2个球放入乙箱中,充分混合后,再从乙箱中取出2个球放回甲箱,求甲箱中白球个数没有减少的槪率.
分析 (1)记“获胜”为事件A,利用相互独立事件概率乘法公式能求出“获胜”的概率小于0.5.
(2)设取出的白球的个数为变量为X,则X的可能取值为1,2,3,4,分别求出相应的概率,由此能求出X的分布列和期望.
(3)记“甲箱中白球队个数没有减少”为事件B,利用相互独立事件概率乘法公式、互斥事件概率加法公式能求出甲箱中白球个数没有减少的槪率.
解答 解:(1)我认为“获胜”的概率小于0.5.
理由如下:
记“获胜”为事件A,
则P(A)=$\frac{4}{7}×\frac{3}{5}=\frac{12}{35}$<0.5,
∴“获胜”的概率小于0.5.
(2)设取出的白球的个数为变量为X,
则X的可能取值为1,2,3,4,
P(X=1)=$\frac{{C}_{4}^{1}{C}_{3}^{3}}{{C}_{7}^{4}}$=$\frac{12}{35}$,
P(X=2)=$\frac{{C}_{4}^{2}{C}_{3}^{2}}{{C}_{7}^{4}}$=$\frac{18}{35}$,
P(X=3)=$\frac{{C}_{4}^{3}{C}_{3}^{1}}{{C}_{7}^{4}}$=$\frac{12}{35}$,
P(X=4)=$\frac{{C}_{4}^{4}{C}_{3}^{0}}{{C}_{7}^{4}}$=$\frac{1}{35}$,
∴X的分布列为:
| X | 1 | 2 | 3 | 4 |
| P | $\frac{4}{35}$ | $\frac{18}{35}$ | $\frac{12}{35}$ | $\frac{1}{35}$ |
(3)记“甲箱中白球队个数没有减少”为事件B,
则P(B)=$\frac{{C}_{3}^{2}}{{C}_{7}^{2}}+\frac{{C}_{4}^{1}{C}_{3}^{1}}{{C}_{7}^{2}}+\frac{{C}_{4}^{2}+{C}_{4}^{1}{C}_{3}^{1}}{{C}_{7}^{2}}+\frac{{C}_{4}^{2}}{{C}_{7}^{2}}•\frac{{C}_{5}^{2}}{{C}_{7}^{2}}$=$\frac{113}{147}$.
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望,相互独立事件概率乘法公式、互斥事件概率加法公式等基础知识,考查推理论证能力、数据处理能力,考查化归与转化思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若复数z1,z2在复平面内的对应点关于虚轴对称,且z1=1+i,则z2=( )
| A. | 1+i | B. | 1-i | C. | -1-i | D. | -1+i |
19.已知命题
p1:函数f(x)=ex-e-x在R上单调递增
p2:函数g(x)=ex+e-x在R上单调递减
则在命题q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2和q4:p1∧(¬p2)中,真命题是( )
p1:函数f(x)=ex-e-x在R上单调递增
p2:函数g(x)=ex+e-x在R上单调递减
则在命题q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2和q4:p1∧(¬p2)中,真命题是( )
| A. | q1,q3 | B. | q2,q3 | C. | q1,q4 | D. | q2,q4 |
3.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点分別为A,B,点M,N是椭圆C上关于长轴对称的两点,若直线AM与BN相交于点P,则点P的轨迹方程是( )
| A. | x=±a(y≠0) | B. | y2=2b(|x|-a)(y≠0) | ||
| C. | x2+y2=a2+b2(y≠0) | D. | $\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(y≠0) |
20.执行如图所示的程序框图,则输出的S值是( )


| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -1 | D. | 4 |
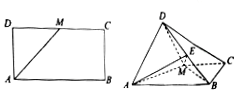 如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 如图椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左顶点A的距离为4+2$\sqrt{2}$.
如图椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左顶点A的距离为4+2$\sqrt{2}$.