题目内容
2.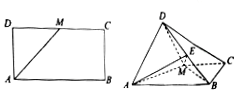 如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.(1)求证:AD⊥BM;
(2)若点E是线段DB上的一动点,问点E在何位置时,二面角E-AM-D的余弦值为$\frac{{\sqrt{2}}}{2}$.
分析 (1)推导出BM⊥AM,从而BM⊥平面ADM,由此能证明AD⊥BM.
(2)以O为原点,OA为x轴,ON为y轴,OD为z轴,建立空间直角坐标系,利用向量法能求出E为BD的三等分点.
解答 证明:(1)∵长方形ABCD中,$AB=2\sqrt{2}$,$AD=\sqrt{2}$,M为DC的中点,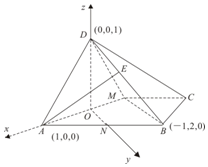
∴AM=BM=2,∴BM⊥AM.
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM?平面ABCM,
∴BM⊥平面ADM,
∵AD?平面ADM,∴AD⊥BM.
(2)以O为原点,OA为x轴,ON为y轴,OD为z轴,
建立如图所示的直角坐标系
设$\overrightarrow{DE}=λ\overrightarrow{DB}$,则平面AMD的一个法向量$\overrightarrow n=({0,1,0})$,
$\overrightarrow{ME}=\overrightarrow{MD}+λ\overrightarrow{DB}$=(1-λ,2λ,1-λ),$\overrightarrow{AM}=({-2,0,0})$,
设平面AME的一个法向量$\overrightarrow m=({x,y,z})$,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AM}=0}\\{\overrightarrow{m}•\overrightarrow{ME}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}2x=0\\ 2λy+({1-λ})z=0\end{array}\right.$
取y=1,得x=0,y=1,$z=\frac{2λ}{λ-1}$,∴$\overrightarrow m=({0,1,\frac{2λ}{λ-1}})$,
∵$|{cos\left?{\overrightarrow m,\overrightarrow n}\right>}|$=$\frac{{|{\overrightarrow m•\overrightarrow n}|}}{{|{\overrightarrow m}||{\overrightarrow n}|}}=\frac{{\sqrt{2}}}{2}$.∴得$λ=\frac{1}{3}$或λ=-1,经检验得$λ=\frac{1}{3}$满足题意.
∴E为BD的三等分点.
点评 本题考查线线垂直的证明,考查满足条件的点位置的判断与求法,考查空间中线线、线面、面面的位置关系等基础知识,考查推理论证能力、数据处理能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案| A. | 若α⊥β,a?α,则a⊥β | B. | 若α⊥γ,β⊥γ,则α∥β | ||
| C. | 若α∥β,a?α,b?β,则a∥b | D. | 若m⊥α,m∥n,n∥β,则α⊥β |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | ab<b2 | C. | ac2<bc2 | D. | |a|>|b| |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | ?x0∈R,sinx0+cos0=$\frac{3}{2}$ | |
| B. | 已知X服从正态分布N(0,σ2),且p(-2<X≤2)=0.6,则P(X>2)=0.2 | |
| C. | 已知a,b为实数,则a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| D. | 命题“?x∈R,x2-x+1>0”的否定是“?x0∈R,x2-x+1<0” |
| 班别 | A | B | C | D |
| 人数 | 45 | 60 | 30 | 15 |
(I )求各班参加竞赛的人数:
(II) 若B班每位参加竞赛的同学对每个题目答对的概率均为p,求B班恰好有2位同学获得奖品的概率;
(III) 若这10个题目,小张同学只有2个答不对,记小张答对的题目数为X,求X的分布列及数学期望E(X)