题目内容
2. 如图椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左顶点A的距离为4+2$\sqrt{2}$.
如图椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左顶点A的距离为4+2$\sqrt{2}$.(1)求椭圆C的标准方程;
(2)设P为椭圆C上位于x轴上方的点,直线PA交y轴于点M,过点F作MF的垂线,交y轴于点N.
(i)当直线PA的斜率为$\frac{1}{2}$时,求△FMN的外接圆的方程;
(ii)设直线AN交椭圆C于另一点Q,求△APQ的面积的最大值.
分析 (1)由椭圆的离心率可知:a=$\sqrt{2}$c,且a+c=4+2$\sqrt{2}$,即可求得a和b的值,b2=a2-c2=8,即可求得椭圆方程;
(2)(i)由直线FN的方程为y=$\frac{2\sqrt{2}}{4k}$(x-2$\sqrt{2}$),则N(0,-$\frac{2}{k}$),k=$\frac{1}{2}$时,求得MF⊥FN,则圆心为(0,-1),半径为3,即可求得△FMN的外接圆的方程;
(ii)设直线PA的方程为y=k(x+4),代入椭圆方程,求得P点坐标,同理即可求得Q点坐标,根据三角形的面积公式,利用基本不等式的性质,即可求得△APQ的面积的最大值.
解答 解:(1)由椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,则a=$\sqrt{2}$c,①
右焦点F到左顶点A的距离为4+2$\sqrt{2}$,即a+c=4+2$\sqrt{2}$,②
解得:$\left\{\begin{array}{l}{a=4}\\{c=2\sqrt{2}}\end{array}\right.$,b2=a2-c2=8,
∴椭圆C的标准方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{8}=1$;
(2)由题可设直线PA的方程为y=k(x+4),k>0,则M(0,4k),
∴直线FN的方程为y=$\frac{2\sqrt{2}}{4k}$(x-2$\sqrt{2}$),则N(0,-$\frac{2}{k}$),
(i)当直线PA的斜率为$\frac{1}{2}$,即k=$\frac{1}{2}$时,M(0,2),N(0,-4),F(2$\sqrt{2}$,0),
则$\overrightarrow{MF}$=(2$\sqrt{2}$,-2),$\overrightarrow{FN}$=(-2$\sqrt{2}$,-4),
由$\overrightarrow{MF}$•$\overrightarrow{FN}$=-8+8=0,
∴MF⊥FN,则圆心为(0,-1),半径为3,
△FMN的外接圆的方程x2+(y+1)2=9;
(ii)联立$\left\{\begin{array}{l}{y=k(x+4)}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{8}=1}\end{array}\right.$,消去y,整理得,(1+2k2)x2+16k2x+32k2-16=0,
解得x1=-4或x2=$\frac{4-8{k}^{2}}{1+2{k}^{2}}$,则P($\frac{4-8{k}^{2}}{1+2{k}^{2}}$,$\frac{8k}{1+2{k}^{2}}$),
直线AN的方程为y=$\frac{1}{2k}$(x+4),同理可得,Q($\frac{8{k}^{2}-4}{1+2{k}^{2}}$,-$\frac{8k}{1+2{k}^{2}}$),
∴P,Q关于原点对称,即PQ过原点.
∴△APQ的面积S=$\frac{1}{2}$•丨OA丨(yP-yQ)=2×$\frac{16k}{1+2{k}^{2}}$=$\frac{32}{2k+\frac{1}{k}}$≤$\frac{32}{2\sqrt{2k×\frac{1}{k}}}$=8$\sqrt{2}$,
当且仅当2k=$\frac{1}{k}$,即k=$\frac{\sqrt{2}}{2}$时,取“=”.
∴△APQ的面积的最大值为8$\sqrt{2}$.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,向量数量积的坐标运算,三角形的面积公式,基本不等式的性质,考查计算能力,属于中档题.

| 广告费用x | 2 | 3 | 4 | 5 |
| 销售额y | 26 | 39 | 49 | 54 |
| A. | 63.6 | B. | 65.5 | C. | 72 | D. | 67.7 |
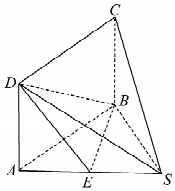 如图,在四棱锥S-ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,$SC=\sqrt{13}$.
如图,在四棱锥S-ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,$SC=\sqrt{13}$.