题目内容
19.已知命题p1:函数f(x)=ex-e-x在R上单调递增
p2:函数g(x)=ex+e-x在R上单调递减
则在命题q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2和q4:p1∧(¬p2)中,真命题是( )
| A. | q1,q3 | B. | q2,q3 | C. | q1,q4 | D. | q2,q4 |
分析 先判断命题p1,p2的真假,进而根据复合命题真假判断的真值表,可得答案.
解答 解:函数y=ex在R上单调递增,y=-e-x在R上单调递减,
故函数f(x)=ex-e-x在R上单调递增,
即p1为真命题;
函数g(x)=ex+e-x在[0,+∞)上单调递增,
即p2为假命题;
则命题q1:p1∨p2为真命题,
q2:p1∧p2为假命题,
q3:(¬p1)∨p2为假命题,
q4:p1∧(¬p2)为真命题,
故选:C
点评 本题以命题的真假判断与应用为载体,考查了复合命题,函数的单调性,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.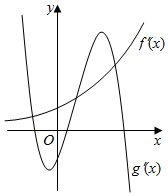 定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)-g(x)极值点的情况是( )
定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)-g(x)极值点的情况是( )
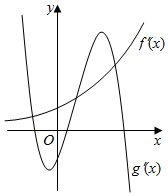 定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)-g(x)极值点的情况是( )
定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)-g(x)极值点的情况是( )| A. | 只有三个极大值点,无极小值点 | B. | 有两个极大值点,一个极小值点 | ||
| C. | 有一个极大值点,两个极小值点 | D. | 无极大值点,只有三个极小值点 |
10.如果a<b<0,那么下列不等式成立的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | ab<b2 | C. | ac2<bc2 | D. | |a|>|b| |
7.下列命题中,正确的是( )
| A. | ?x0∈R,sinx0+cos0=$\frac{3}{2}$ | |
| B. | 已知X服从正态分布N(0,σ2),且p(-2<X≤2)=0.6,则P(X>2)=0.2 | |
| C. | 已知a,b为实数,则a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| D. | 命题“?x∈R,x2-x+1>0”的否定是“?x0∈R,x2-x+1<0” |
14.某年级举办团知识竞赛A、B、C、D四个班报名人数如下:
年级在报名的同学中按分层抽样的方式抽取10名同学参加竞赛,每位参加竞赛的同学从10个关于团知识的题目中随机抽取4个作答,全部答对的同学获得一份奖品.
(I )求各班参加竞赛的人数:
(II) 若B班每位参加竞赛的同学对每个题目答对的概率均为p,求B班恰好有2位同学获得奖品的概率;
(III) 若这10个题目,小张同学只有2个答不对,记小张答对的题目数为X,求X的分布列及数学期望E(X)
| 班别 | A | B | C | D |
| 人数 | 45 | 60 | 30 | 15 |
(I )求各班参加竞赛的人数:
(II) 若B班每位参加竞赛的同学对每个题目答对的概率均为p,求B班恰好有2位同学获得奖品的概率;
(III) 若这10个题目,小张同学只有2个答不对,记小张答对的题目数为X,求X的分布列及数学期望E(X)
9.某产品的广告费用x万元与销售额y万元的统计数据如表:
根据上表可得回归方程$\widehaty=9.4x+a$,据此模型预测,广告费用为6万元时的销售额为( )万元.
| 广告费用x | 2 | 3 | 4 | 5 |
| 销售额y | 26 | 39 | 49 | 54 |
| A. | 63.6 | B. | 65.5 | C. | 72 | D. | 67.7 |