题目内容
1．若复数z1，z2在复平面内的对应点关于虚轴对称，且z1=1+i，则z2=（ ）| A． | 1+i | B． | 1-i | C． | -1-i | D． | -1+i |
分析 利用复数z1，z2在复平面内的对应点关于虚轴对称即可得出．
解答 解：复数z1，z2在复平面内的对应点关于虚轴对称，且z1=1+i，
则z2=-1+i．
故选：D．
点评 本题考查了复数的几何意义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
11．若数列{an}满足a1=1，an+1=nan+1，则第5项a5=（ ）
| A． | 5 | B． | 65 | C． | 89 | D． | 206 |
12．已知m、n为空间两条不同直线，α、β、γ为不同的平面，则下列命题正确的是（ ）
| A． | 若α⊥β，a?α，则a⊥β | B． | 若α⊥γ，β⊥γ，则α∥β | ||
| C． | 若α∥β，a?α，b?β，则a∥b | D． | 若m⊥α，m∥n，n∥β，则α⊥β |
9．
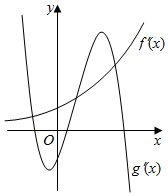定义在R上的函数f（x）和g（x），其各自导函数f′（x）f和g′（x）的图象如图所示，则函数F（x）=f（x）-g（x）极值点的情况是（ ）
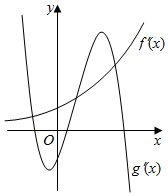定义在R上的函数f（x）和g（x），其各自导函数f′（x）f和g′（x）的图象如图所示，则函数F（x）=f（x）-g（x）极值点的情况是（ ）| A． | 只有三个极大值点，无极小值点 | B． | 有两个极大值点，一个极小值点 | ||
| C． | 有一个极大值点，两个极小值点 | D． | 无极大值点，只有三个极小值点 |
13．已知p：a＞2，q：a2＞4，则￢p是￢q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
10．如果a＜b＜0，那么下列不等式成立的是（ ）
| A． | $\frac{1}{a}＜\frac{1}{b}$ | B． | ab＜b2 | C． | ac2＜bc2 | D． | |a|＞|b| |