题目内容
3.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点分別为A,B,点M,N是椭圆C上关于长轴对称的两点,若直线AM与BN相交于点P,则点P的轨迹方程是( )| A. | x=±a(y≠0) | B. | y2=2b(|x|-a)(y≠0) | ||
| C. | x2+y2=a2+b2(y≠0) | D. | $\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(y≠0) |
分析 求得直线PA的方程及PB的方程,两式相乘,整理即可求得P的轨迹方程.
解答 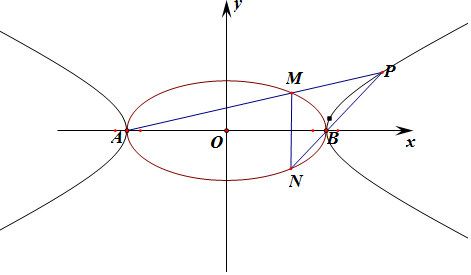 解:由题意可知:A(-a,0),B(a,0),设M(x0,y0),N(x0,-y0),y0≠0,P(x,y),y≠0
解:由题意可知:A(-a,0),B(a,0),设M(x0,y0),N(x0,-y0),y0≠0,P(x,y),y≠0
则直线PA的斜率k=$\frac{{y}_{0}}{{x}_{0}+a}$,则直线PA的方程y=$\frac{{y}_{0}}{{x}_{0}+a}$(x+a),①
同理直线PB的斜率k=$\frac{{y}_{0}}{a-{x}_{0}}$,直线PB的方程y=$\frac{{y}_{0}}{a-{x}_{0}}$(x-a),②
两式相乘:y2=$\frac{{y}_{0}^{2}}{{a}^{2}-{x}_{0}^{2}}$(x2-a2),
由$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$,y02=$\frac{{b}^{2}}{{a}^{2}}$(a2-x02),
则y2=$\frac{{b}^{2}}{{a}^{2}}$(x2-a2),整理得:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)(y≠0),
则点P的轨迹方程$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)(y≠0),
故选D.
点评 本题考查椭圆的标准方程,直线的点斜式方程,考查轨迹方程的求法,考查转化思想,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
13.已知p:a>2,q:a2>4,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.某年级举办团知识竞赛A、B、C、D四个班报名人数如下:
年级在报名的同学中按分层抽样的方式抽取10名同学参加竞赛,每位参加竞赛的同学从10个关于团知识的题目中随机抽取4个作答,全部答对的同学获得一份奖品.
(I )求各班参加竞赛的人数:
(II) 若B班每位参加竞赛的同学对每个题目答对的概率均为p,求B班恰好有2位同学获得奖品的概率;
(III) 若这10个题目,小张同学只有2个答不对,记小张答对的题目数为X,求X的分布列及数学期望E(X)
| 班别 | A | B | C | D |
| 人数 | 45 | 60 | 30 | 15 |
(I )求各班参加竞赛的人数:
(II) 若B班每位参加竞赛的同学对每个题目答对的概率均为p,求B班恰好有2位同学获得奖品的概率;
(III) 若这10个题目,小张同学只有2个答不对,记小张答对的题目数为X,求X的分布列及数学期望E(X)
18.已知平面α及直线a,b,则下列说法正确的是( )
| A. | 若直线a,b与平面α所成角都是30°,则这两条直线平行 | |
| B. | 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直 | |
| C. | 若直线a,b平行,则这两条直线中至少有一条与平面α平行 | |
| D. | 若直线a,b垂直,则这两条直线与平面α不可能都垂直 |