题目内容
6．已知函数f（x）=$\frac{（x-2）（x+a）}{{x}^{2}}$为偶函数，则a=2．分析 依据f（x）=f（-x）求出a的值．
解答 解：∵f（x）=$\frac{（x-2）（x+a）}{{x}^{2}}$为偶函数，
∴f（x）=f（-x），即$\frac{（-x-2）（-x+a）}{{x}^{2}}$=$\frac{（x-2）（x+a）}{{x}^{2}}$
∴a=2．
故答案为：2
点评 本题主要考查函数的奇偶性的运用．属基础题．
练习册系列答案
相关题目
17．有下述说法：①a＞b＞0是a2＞b2的充分不必要条件．②a＞b＞0是$\frac{1}{a}＜\frac{1}{b}$的充要条件．③a＞b＞0是a3＞b3的充要条件．则其中正确的说法有（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
14．某年级举办团知识竞赛A、B、C、D四个班报名人数如下：
年级在报名的同学中按分层抽样的方式抽取10名同学参加竞赛，每位参加竞赛的同学从10个关于团知识的题目中随机抽取4个作答，全部答对的同学获得一份奖品．
（I ）求各班参加竞赛的人数：
（II） 若B班每位参加竞赛的同学对每个题目答对的概率均为p，求B班恰好有2位同学获得奖品的概率；
（III） 若这10个题目，小张同学只有2个答不对，记小张答对的题目数为X，求X的分布列及数学期望E（X）
| 班别 | A | B | C | D |
| 人数 | 45 | 60 | 30 | 15 |
（I ）求各班参加竞赛的人数：
（II） 若B班每位参加竞赛的同学对每个题目答对的概率均为p，求B班恰好有2位同学获得奖品的概率；
（III） 若这10个题目，小张同学只有2个答不对，记小张答对的题目数为X，求X的分布列及数学期望E（X）
1．已知等比数列{an}的前n项和Sn=$\frac{{4}^{n}-1}{3}$，则数列{$\sqrt{{a}_{n}}$}的前n项和Tn=（ ）
| A． | 2n-1 | B． | $\sqrt{\frac{{4}^{n}-1}{3}}$ | C． | $\frac{{2}^{n}-1}{3}$ | D． | $\frac{{2}^{n+1}-3}{3}$ |
18．已知平面α及直线a，b，则下列说法正确的是（ ）
| A． | 若直线a，b与平面α所成角都是30°，则这两条直线平行 | |
| B． | 若直线a，b与平面α所成角都是30°，则这两条直线不可能垂直 | |
| C． | 若直线a，b平行，则这两条直线中至少有一条与平面α平行 | |
| D． | 若直线a，b垂直，则这两条直线与平面α不可能都垂直 |
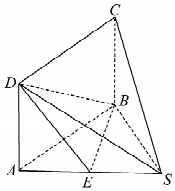如图，在四棱锥S-ABCD中，四边形ABCD为矩形，E为SA的中点，SB=2，BC=3，$SC=\sqrt{13}$．