题目内容
已知函数f(x)=
,若?x∈R,f(x)≤ax+2(a∈R),则a的最大值为 .
|
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用
分析:作出函数f(x)的图象,令y=ax+2,则图象为直线且经过(0,2),将直线绕着点(0,2)旋转时,当直线与y=-x2-2x,x≤0的图象相切时,直线在函数f(x)的图象上方,且此时斜率a最大,联立直线方程和抛物线方程,消去y,运用判别式为0,通过图象观察,舍去负值.
解答:
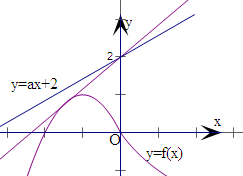 解:作出函数f(x)的图象,
解:作出函数f(x)的图象,
令y=ax+2,则图象为直线且经过(0,2),
将直线绕着点(0,2)旋转时,当直线与y=-x2-2x,x≤0的图象相切时,直线在函数f(x)的图象上方,且此时斜率a最大,
联立直线y=ax+2和y=-x2-2x,消去y得,x2+(a+2)x+2=0,
由判别式为0,即有(a+2)2-8=0解得a=-2+2
或-2-2
由图象可知a=-2-2
不成立,舍去.
故答案为:2
-2.
 解:作出函数f(x)的图象,
解:作出函数f(x)的图象,令y=ax+2,则图象为直线且经过(0,2),
将直线绕着点(0,2)旋转时,当直线与y=-x2-2x,x≤0的图象相切时,直线在函数f(x)的图象上方,且此时斜率a最大,
联立直线y=ax+2和y=-x2-2x,消去y得,x2+(a+2)x+2=0,
由判别式为0,即有(a+2)2-8=0解得a=-2+2
| 2 |
| 2 |
由图象可知a=-2-2
| 2 |
故答案为:2
| 2 |
点评:本题考查分段函数的图象和运用,考查数形结合的思想方法,以及直线与抛物线相切的条件,考查运算能力,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
若集合M={x|x-3<0,x∈N},则下列四个命题中,正确的命题是( )
| A、0∉M | B、{0}∈M |
| C、{1}⊆M | D、1⊆M |
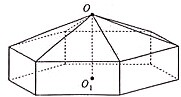 请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积为16
请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积为16