题目内容
当x∈[-2，2]时，|2x-1|-3|x+1|-m≥0有解，求m的取值范围．
考点：绝对值不等式的解法
专题：数形结合,函数的性质及应用,不等式的解法及应用
分析：建立函数y=|2x-1|-3|x+1|，只要求出函数在x∈[-2，2]的最小值即可．
解答：
解：设函数y=|2x-1|-3|x+1|=
，
观察图象如图
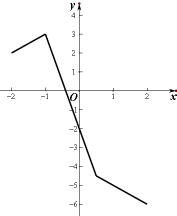
当x∈[-2，2]时，要使|2x-1|-3|x+1|-m≥0有解，只要|2x-1|-3|x+1|≥m能成立，只要m小于等于y的最大值，
由图象可知函数的最大值为x=-1时的函数值为3，所以m≤3．．
|
观察图象如图
当x∈[-2，2]时，要使|2x-1|-3|x+1|-m≥0有解，只要|2x-1|-3|x+1|≥m能成立，只要m小于等于y的最大值，
由图象可知函数的最大值为x=-1时的函数值为3，所以m≤3．．
点评：本题考查了绝对值不等式的解法；本题巧妙构造函数，集中于函数图象求出最小值，求参数m的范围．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知圆C：（x-1）2+（y-2）2=
，直线l：（2m+1）x+（m+1）y-7m-4=0（m∈R）．
（1）试讨论直线l与圆C的位置关系，并叙述理由；
（2）求直线被圆C截得的弦长最小时l的方程．
| 25 |
| 4 |
（1）试讨论直线l与圆C的位置关系，并叙述理由；
（2）求直线被圆C截得的弦长最小时l的方程．
某班共有6个数学研究性学习小组，本学期初有其它班的3名同学准备加入到这6个小组中去，则这3名同学恰好有2人安排在同一个小组的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|