题目内容
定义min{a,b}为两数中最小数,若f(x)=min{4x+1,x+2},画出函数f(x)的图象并求出值域.
考点:函数的图象
专题:函数的性质及应用
分析:先求出两直线的交点,再画出函数的图象,先根据符号:min{a,b}的含义化简函数f(x)的表达式,变成分段函数的形式,得求函数的单调区间,再在每一段上求出函数的值域,最后把各段值域取并集.
解答:
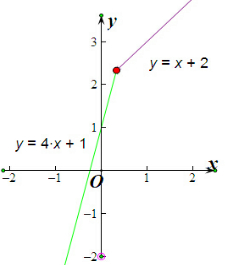 解:由方程4x+1=x+2,
解:由方程4x+1=x+2,
得交点坐标为(
,
),
画出y=4x+1,y=x+1的图象,
观察图象可知,当x≤
时,f(x)=4x+1,
当x>
时,f(x)=x-2,
由图象知,函数的值域为(-∞,+∞)
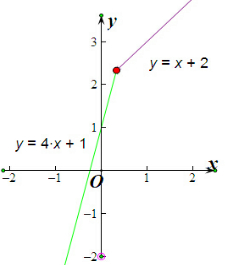 解:由方程4x+1=x+2,
解:由方程4x+1=x+2,得交点坐标为(
| 1 |
| 3 |
| 7 |
| 3 |
画出y=4x+1,y=x+1的图象,
观察图象可知,当x≤
| 1 |
| 3 |
当x>
| 1 |
| 3 |
由图象知,函数的值域为(-∞,+∞)
点评:本题考查用数形结合的方法求函数的解析式、单调区间、值域,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
已知函数f(x)=x2+ln(x+m)与函数g(x)=x2+ex-
(x<0)的图象上存在关于y轴对称的点(e为自然对数的底数),则m的取值范围是( )
| 1 |
| 2 |
A、(-∞,
| ||||||
B、(-∞,
| ||||||
C、(-
| ||||||
D、(-
|
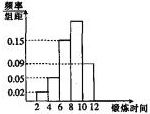 某校友200位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10]小时内的人数为( )
某校友200位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10]小时内的人数为( )| A、76 | B、82 | C、88 | D、95 |