题目内容
3.集合P={x||x|<3,x∈Z},集合Q={y|y=x+1,x∈P},则P∩Q=( )| A. | {-1,-2,0,1} | B. | {-1,0,1,2} | C. | {0,1,2,3} | D. | {-1,1,2,3} |
分析 求出P中不等式解集中的整数解确定出P,进而确定出Q,找出P与Q的交集即可.
解答 解:∵P={x||x|<3,x∈Z}={x|-3<x<3,x∈Z}={-2,-1,0,1,2},Q={y|y=x+1,x∈P}={-1,0,1,2,3},
∴P∩Q={-1,0,1,2},
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
11.设函数f(x)=$\frac{1}{2}$x2-3x+31nx+3,则下列区间中有零点的是( )
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,2) | D. | (2,e) |
18.设x,y满足约束条件$\left\{\begin{array}{l}{x-3y+4≥0,}&{\;}\\{x+2y-1≥0,}&{\;}\\{3x+y-8≤0.}&{\;}\end{array}\right.$,则z=2x-y的最小值与最大值分别为( )
| A. | -3与7 | B. | 2与3 | C. | 2与7 | D. | 3与7 |
8.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(1,1),若($\overrightarrow{a}$+$λ\overrightarrow{b}$)⊥$\overrightarrow{b}$,则λ等于( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
13.下列方程表示焦点在x轴上的椭圆是( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 |
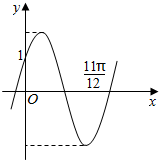 函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示
函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示