题目内容
18.设x,y满足约束条件$\left\{\begin{array}{l}{x-3y+4≥0,}&{\;}\\{x+2y-1≥0,}&{\;}\\{3x+y-8≤0.}&{\;}\end{array}\right.$,则z=2x-y的最小值与最大值分别为( )| A. | -3与7 | B. | 2与3 | C. | 2与7 | D. | 3与7 |
分析 先画出满足条件的平面区域,求出A,B的坐标,由z=2x-y得:y=2x-z,通过读图求出z的最值即可.
解答 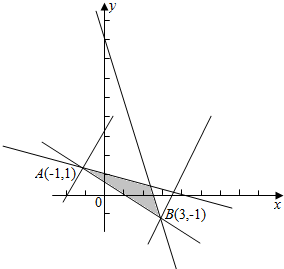 解:画出满足条件的平面区域,如图示:
解:画出满足条件的平面区域,如图示:
由$\left\{\begin{array}{l}{x-3y+4=0}\\{x+2y-1=0}\end{array}\right.$,解得A(-1,1),
由$\left\{\begin{array}{l}{x+2y-1=0}\\{3x+y-8=0}\end{array}\right.$,解得:B(3,-1),
由z=2x-y得:y=2x-z,
显然直线过A(-1,1)时,z最小,最小值是-3,
直线过B(3,-1)时,z最大,最大值是7,
故选:A.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
13.已知直线x+4y=2与x轴,y轴分别交于A,B两点,若动点P(a,b)在线段AB上,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
3.集合P={x||x|<3,x∈Z},集合Q={y|y=x+1,x∈P},则P∩Q=( )
| A. | {-1,-2,0,1} | B. | {-1,0,1,2} | C. | {0,1,2,3} | D. | {-1,1,2,3} |
10.设奇函数f(x)在(0,+∞)上为减函数,且f(1)=0,则不等式$\frac{2f(x)-f(x)}{3x}$<0的解集为( )
| A. | (-1,0)∪(1,+∞) | B. | (-∞,-1)∪(0,1) | C. | (-∞,-1)∪(1,+∞) | D. | (-1,0)∪(0,1) |
8.在0°~360°范围内,与-30°终边相同的角是( )
| A. | 30° | B. | 60° | C. | 210° | D. | 330° |