题目内容
已知函数f(x)满足f(x)=f(-x),且当x∈(-∞,0)时,f(x)+xf′(x)<0成立,若a=(20.1)•f(20.1),b=(ln2)•f(ln2),c=(log2
)•f(log2
),则a,b,c的大小关系是( )
| 1 |
| 8 |
| 1 |
| 8 |
| A、a>b>c |
| B、c>b>a |
| C、a>c>b |
| D、c>a>b |
考点:利用导数研究函数的单调性,不等式比较大小
专题:导数的综合应用
分析:构造函数h(x)=xf(x),由y=f(x)是R上的偶函数,y=x是R上的奇函数,得h(x)=xf(x)是R上的奇函数,h(x)在(-∞,0)递减,在(0,+∞)递减,得3>20.2>1,0<ln2<1,|log2
|>20.2>ln2.推出结果.
| 1 |
| 8 |
解答:
解:构造函数h(x)=xf(x),由y=f(x)是R上的偶函数,y=x是R上的奇函数,
得h(x)=xf(x)是R上的奇函数,
又x∈(-∞,0)时,h′(x)=f(x)+xf′(x)<0成立,
∴h(x)在(-∞,0)递减,在(0,+∞)递减,
∵3>20.2>1,0<ln2<1,∴|log2
|=3>20.2>ln2,
a=(20.1)•f(20.1),b=(ln2)•f(ln2),c=(log2
)•f(log2
)
即b>a>c,
故选:D.
得h(x)=xf(x)是R上的奇函数,
又x∈(-∞,0)时,h′(x)=f(x)+xf′(x)<0成立,
∴h(x)在(-∞,0)递减,在(0,+∞)递减,
∵3>20.2>1,0<ln2<1,∴|log2
| 1 |
| 8 |
a=(20.1)•f(20.1),b=(ln2)•f(ln2),c=(log2
| 1 |
| 8 |
| 1 |
| 8 |
即b>a>c,
故选:D.
点评:本题考查了函数的单调性,导数的应用,函数的奇偶性,是一道综合题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
设f(x)=
,则f(f(5))=( )
|
| A、-1 | B、1 | C、-2 | D、2 |
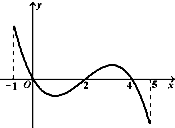 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题: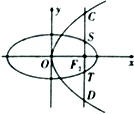 如图,椭圆E:
如图,椭圆E: