题目内容

已知：椭圆C1：
x2
4
+
y2
1
=1，椭圆C2：
y2
8
+
x2
2
=1，则在这两个椭圆的a、b、c、e四个量中，相同的量是
 
．
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：求出两个椭圆中的a、b、c、e四个量，即可得到相同的量．
解答： 解：椭圆C1：
x2
4
+
y2
1
=1中，a=2、b=1、c=
3
、e=
3
2
．
椭圆C2：
y2
8
+
x2
2
=1，a=2
2
、b=
2
、c=
6
、e=
6
2
2
=
3
2
．
显然相等的量是e．
故答案为：e．
点评：本题考查椭圆的基本性质，基本知识的考查．
练习册系列答案
相关题目
已知△ABC的内角A，B，C对边分别为a，b，c，若cosC=
a
b
，且sinC=
3
2
sinB，则△ABC的内角A=
 
．
已知函数f（x）=3x2-1的值域为[1，+∞），定义域为A，g（x）=lg[（x-a-1）（2a-x）]（a＜1）的定义域为B．
（1）求A；
（2）若B⊆A，求a的取值范围．
在ABC中，a，b，c为角A，B，C所对的边，sin2C+sinAsinB=sin2A+sin2B
（1）求角C的大小；
（2）若c=2，且sinC+sin（B-A）=2sin2A，求△ABC的面积．
已知三次函数f（x）=
1
3
ax3+
1
2
bx2-6x+1（x∈R），a，b为实数．
（1）若a=3，b=3时，求函数f（x）的极大值和极小值；
（2）设函数g（x）=f′（x）+7有唯一零点，若b∈[1，3]，求
g(1)
g′(0)
的取值范围．
已知函数f（x）满足f（x）=f（-x），且当x∈（-∞，0）时，f（x）+xf′（x）＜0成立，若a=（20.1）•f（20.1），b=（ln2）•f（ln2），c=（log2
1
8
）•f（log2
1
8
），则a，b，c的大小关系是（　　）
A、a＞b＞c
B、c＞b＞a
C、a＞c＞b
D、c＞a＞b
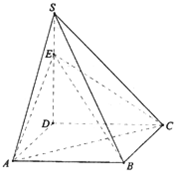如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=a，点E是SD上的点，且DE=λa（0＜λ≤1）．请利用空间向量解决下列问题：
（1）当λ=
2
3
时，求异面直线AE和SC所成的角的余弦值；
（2）若直线AB和平面AEC所成的角为30°，求λ的值．
已知函数f﹙x﹚=﹙1+x﹚e-2x，当x∈[0，1]时，求证：1-x≤f﹙x﹚≤
1
x+1
．
已知O为△ABC内一点，满足
OA
+
OB
+
OC
=
0
．若
AB
+
AC
=λ
AO
，则实数λ=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网